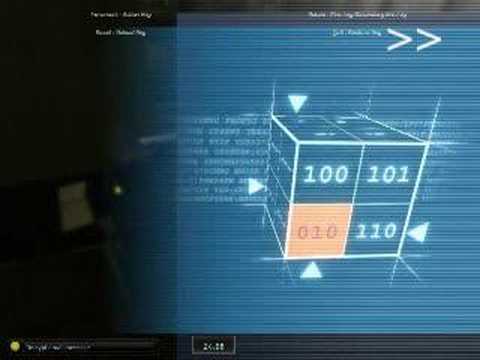
Würfelrätsel in Splinter Cell Double Agent
Im Computerspiel »Splinter Cell: Double Agent« spielt man den NSA Geheimagenten Sam Fischer, der unbemerkt hinter feindlichen Linien aufklären soll. Dabei gibt es wie in vielen Computerspielen so Rätsel, die man lösen muss. Das »Hacken« ist meist irgendein Minispiel, das nicht wirklich viel Können erfordert.
Umso erstaunter war ich, als eines der kleinen Spiele ein wirklich schweres Rätsel war. Man hatte einen Würfel, der auf jeder Seite vier Felder hatte. Man sollte jedes der Felder mit einer dreistelligen Binärzahl füllen und dabei diese Zahl nicht innerhalb eines Umfanges wiederholen. So sah das im Spiel aus:
Das ist gar nicht so leicht. Die dreistelligen Binärzahlen sind die Zahlen von 0 bis 7, es gibt also 8 Stück. Und in jedem Umfang um den Würfel hat man vier Seiten, und dann zwei Felder dort. Man kann also beim ersten Umfang einfach hochzählen. Aber dann?
Es ist hilfreich den Würfel erstmal aufzuschneiden und die Felder zu benennen. So kann man dann besser darüber nachdenken, als wenn man sich das alles noch in 3D vorstellen muss. Die Namen sind willkürlich, ich habe jetzt einfach 24 Buchstaben genommen:
Nun kann man einzeichnen, welche Umfänge es gibt. Es sind insgesamt sechs Stück, hier alle mit unterschiedlichen Farben markiert:
Mit dieser Abbildung kann man auch das Rätsel noch ein bisschen besser verstehen. Wir müssen die Zahlen von 0 bis 7 so den Buchstaben zuordnen, sodass entlang jeder bunten Linie jede Zahl nur einmal vorkommt. Es ist also Sudoku, nur auf einer Würfeloberfläche. Aber ansonsten genau das gleiche Prinzip.
Die Lösung ist nicht eindeutig, weil man gewisse Freiheiten hat, wie man genau dreht. Eine mögliche Lösung ist in diesem Artikel gezeigt, eine andere Lösung in diesem anderen Artikel. Aber mich interessiert weniger die Lösung als der Lösungsweg und die Strukturen, die man dabei findet.
Ein bisschen Orientierung kann uns die Gruppentheorie geben. Wir haben insgesamt 24 Felder und 8 Zahlen. Weil das Problem komplett drehsymmetrisch ist, und keine Zahl ausgezeichnet ist, werden wir jede Zahl gleich oft nutzen müssen, also drei Mal. Das ist schon einmal hilfreich. Wir können das ganze Problem also auch so angehen, dass wir drei Teile zu je acht Feldern müssen, oder acht Teile zu je drei Feldern.
Wir können die effektiven Verbindungen aller Felder mit anderen Feldern einmal als Graphen darstellen. Dabei habe ich alle Felder, die mit A verbunden sind, grau markiert.
Man kann schon sehen, dass das ganze eine interessante und symmetrische Struktur hat. Das konnte man aus dem abgerollten Würfel nicht so gut erkennen.
Noch cooler ist es allerdings, wenn man die Verbindungen nach den Umfängen einfärbt. Dann kann man sehen, wie die sechs Umfänge da jeweils einen Cluster bilden. Innerhalb eines Clusters dürfen die Zahlen nur einmal vorkommen.
Wir haben sechs Umfänge. Jede Zahl müssen wir dreimal unterbringen. Wir müssen also pro zwei Umfänge alle Zahlen unterbringen. Wir sehen auch, dass die Umfänge überlappen, aber immer nur zwei davon.
Wenn wir jetzt noch einmal jene Knoten markieren, die mit A verbunden sind, dann sieht das hier so aus:
Wir können also der A die 0 zuweisen, und dann müssen wir noch zwei weitere Knoten wählen. Wegen der Symmetrie scheint es am sinnvollsten, wir nehmen noch K und R. Man kann das ganze systematisch so machen, dass man einfach entlang von einem Umfang die Zahlen 0 bis 7 vergibt, und dann bei den anderen schaut, welche beiden anderen Felder im 120° Winkel dazu liegen.
Wir können auch erstmal den grünen Umfang komplett von 0 bis 7 füllen. Und zwar so, dass jene Felder mit Verbindung nach cyan die 0 bis 3 bekommen, die zu pink die 4 bis 7. Dann gehen wir zu jenen, die pink-gelb sind und können dort die 0 bis 3 wieder nutzen. Dann bei gelb-rot die 4 bis 7, rot-blau die 0 bis 3 und dann hat blau-cyan schon automatisch die 4 bis 7, sodass es nicht im Konflikt zu den 0 bis 3 von grün-cyan steht.
So sieht man auch, wie viele Freiheiten das Problem hat. Man kann nämlich zum einen Willkürlich die acht Zahlen in zwei Gruppen aufteilen, da gibt es schon 1680 Möglichkeiten. Und dann können wir in jedem Schritt die Reihenfolge der vier Zahlen pro neuer Farbkombination auch frei Wählen, macht wieder 24 Möglichkeiten. Bei sechs Farbkombinationen müssten das 321.052.999.680 Möglichkeiten sein.
Andererseits sind alle dieser Lösungen korrekt, von daher kann man frei Wählen. Bei der Konstruktion einer Lösung sind diese vielen Möglichkeiten meist hinderlich, weil man keine externe Orientierung hat und beliebig anfangen kann.
Für ein Computerspiel, das sich wahrscheinlich an Teenager richtet, finde ich das ein ziemlich schweres Problem. Man hatte im Spiel dafür zehn Minuten Zeit. Das kommt mir schon sehr sportlich vor, wenn man nicht zufällig die Intuition dafür hat. Es war aber auch eine Zusatzmission, die man nicht schaffen musste. Vielleicht hat man sich daher für ein schweres Rätsel entschieden.