Backtracking in Railroad Ink
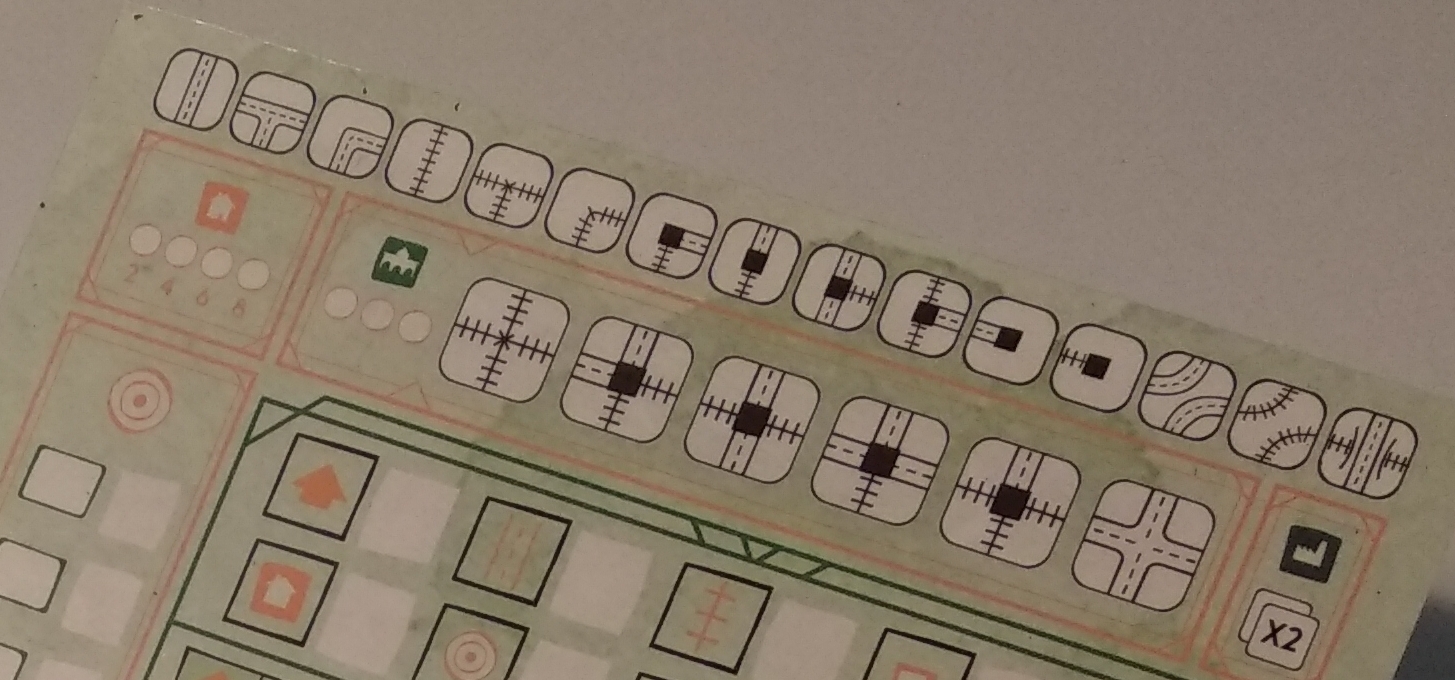
One of my favorite board games is “Railroad Ink”. One has to build a rail and road network on a square grid using the building blocks shown on dice. During the game, my player mat looks like this:
My drawing style is minimalistic. Solid lines are rail lines, dotted lines are roads, and black squares are rail stations. You can see the nice versions of the building blocks on the very top of the player mat.
The game works by rolling dice with the building blocks, usually four of them. One then has to add all blocks to the board. Each player has their own board, so the various players don't really interact with each other. There are a few additional rules. For instance one needs to connect a piece to some existing part of the network or one of the external connections at the edge of the grid. Connections can be left hanging, but they must not conflict (no rail becoming a road).
One scores points for connecting as many external connections with one connected part of the roads and rails that one builds. One can have multiple independent meshes of connections, each gets points separately. Then there are some specials like extra points for constructing in the white middle zone, for connecting housing areas (orange house icon) with a rail station. Open ends deduct one point.
The longest rail and the longest road also get scored, one point per tile. This is again a game where the “longest simple path” from graph theory shows up. Either these games pick me, or I pick these games.
While you play the game, you have to put in the building blocks such that you have enough open ends to continue flexibly. Yet you don't want open ends at the end of the game (seven rounds). You want to connect as many external connections into a single mesh as possible. You want to have a really long road and a really long rail. This makes it hard, because in each round you only get four random building blocks:
One could think of theoretical layouts which connect everything, like this one:
But that's actually impossible to build. One doesn't have so many four-way hubs, they are limited to four out of the available six unique ones per game.
Backtracking
I had recently used backtracking to beat a fake IQ test, and it might be a good application here as well. One can think of this game as yet another instance of graph search. From each state of the game one has many possibilities. It is a really sparse problem in the sense that at each step in the game only few options are available. There are only a few building blocks, and one can only attach them to a few possibilities in the game. This makes Q-learning not very applicable. Monte Carlo Tree Search seems possible.
I will just try backtracking and see whether one can fill the full board without having open ends. This glosses over the fact that one cannot choose the building blocks from the pool. But it constructs what a “perfect” game could look like.
The game's graphics are minimal, yet beautifully made. As I am a backend and high performance software engineer, I'm not that good with graphics. I thought about trying to make nice graphics for it, but I just started programming. In the first iteration, I just start with two exists. I mark hubs with #, rails with + and road with .. And then the game looks like this with two external rail connections:
#
+
+
#++
The only building blocks that I have put in are the straight rail and the straight road. So after a few steps it looks like this:
#
+
+
#+++++++++++++++++
And after more backtracking, it will try to start from the other external connection and yield this:
#
+
+
+
+
+
+
+
+
+
#++ +
+
+
+
+
+
+
+
So that's nice. It seems that the connection logic works, and that it can also rotate the building blocks correctly.
Adding more building blocks
My definition of building blocks looks pretty technical. I specify a name, then an ASCII art tile image, and then the connectors. There are some building blocks which have multiple connections, but they don't connect all of them to all others (the two curves or the rail-road-overpass). Therefore there are two levels of lists.
unique_tiles = [ Tile( "straight rail", " \n \n+++++\n \n ", [[(Direction.LEFT, TransportType.RAIL), (Direction.RIGHT, TransportType.RAIL)]], ), Tile( "straight road", " \n \n.....\n \n ", [[(Direction.LEFT, TransportType.ROAD), (Direction.RIGHT, TransportType.ROAD)]], ), ]
We can get a list of all possible building blocks from the header of the player mat:
And then I just have to implement all of them. When just adding the curves and T-crossings, one gets meshes like this:
#
+
+
+
+
++++++++
#+++++++++++++++
+
+
+
+
+++++++++++++
+ + +
+ + +
With these more pieces I can fill the full playing field. It starts to look somewhat interesting:
# # #
. + .
. + .
. . + .
. . + .
........ .....#..........
#+++++++++++++++++++++++++++++++++++++++#
#.......................................#
#+++++++++++++++++++++++++++++++++++++++#
........ #..........
. + .
. + .
. + .
. + .
# # #
But it looks really unpleasing.
Making tiles
The programming part is pretty much done, but the ASCII art results are really unpleasing. So I will now make some tiles. I am unsure about just scanning the dice or the player mat, so I will design my own. And here they are:
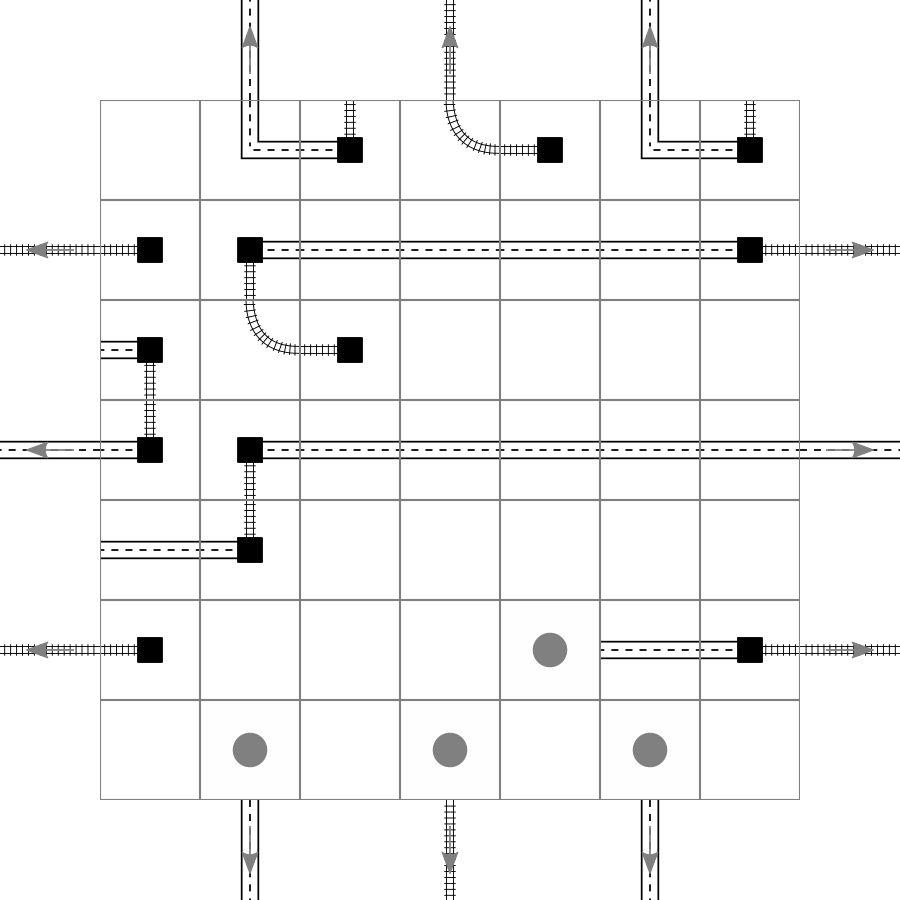
Using these tiles I can now generate much nicer pictures from the backtracking algorithm. With these we can now see game states like these:
The lattice sites with a circle are the ones where one can place a new building block.
Backtracking gets stuck
The problem with backtracking is that it is a depth-first search. This means that it gets stuck in one corner of the state space, and virtually stops exploring. That can be seen very well in this longer video:
As you can see, it will go through the elements in the bottom right corner and tries to fill that with all possible elements. The game has 15 unique building blocks, which can be rotated. One can even be mirrored, so we end up having quite a bunch of possibilities. On a grid with 7×7 sites we have 49 spots to fill. With all rotations we have around 50 building blocks. This then gives a state space size of 177,635,683,940,025,046,467,781,066,894,531,250,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, which is 1.7×10⁸³. That is more than the number of atoms in the visible universe. It is completely out of the question to go through all of them.
Outlook
So one could use backtracking to get to interesting combinations, but it would never get a usable result in time. Therefore this naive algorithm doesn't work for such a complicated problem.
One goal could be to find a configuration which connects all the exits into one mesh and doesn't have open ends. Once the whole board is filled, or seven rounds of four tiles are set, one could evaluate this as a simple binary question. We just go until we find one such solution, or we just let it run to produce more and more of this kind. Such binary questions are perfectly suited for Monte Carlo Tree Search. I might try that out some time later.