Monte Carlo Tree Search for Railroad Ink
In a recent post I looked at the game “Railroad Ink” and how applying a backtracking algorithm to it. Then I have written another post about refactoring that into a tree search library and also have applied a random walk algorithm to Railroad Ink. Then in yet another post I have implemented Monte Carlo tree search (MCTS) and applied it to Tic-Tac-Toe. This algorithm is now also part of the tree search library and can be applied to Railroad Ink. That is what I am going to do in this post.
With all graph searches, one needs to define what one is looking for. In this game there are many different ways to score points. But I am just looking for networks that connect all twelve exits. The problem that I face is that it is very unlikely for a random walk to find such a configuration. So if I define a “win” just by fully reaching this goal, it likely works as bad as a random walk. I would need to give partial rewards. In the pure MCTS framework one just counts wins and playouts. The ratio gives the success. But when there is a draw, one can give 0.5 win points. So this seems to be an avenue where one can introduce partial rewards. I will take the number of exists in the largest cluster, and divide that by 12. This gives a reward between 0.0 and 1.0 and sounds like a promising idea.
The success metric itself is a graph theoretical one, and one needs a graph search algorithm to find it. The problem is that the mesh of roads and rails doesn't need to span a tree, it can also span a graph with cycles. For this I won't write an algorithm myself but could resort to a proper graph library like igraph. This should then try to figure out the connectivity. Alternatively I can use my backtracking algorithm with the additional provision that I don't step on the same lattice site again. This way I would try out all possible non-intersecting paths, which then becomes a feasible problem again. I can then use the backtracking algorithm that I have already programmed for an earlier blog post.
Computing connectivity
When I started with Railroad Ink, I already defined the tiles with connectivity in mind. Take for instance the “overpass” tile. It does connect left and right, as well as up and down, but not all four of them.
I have reflected that in the representation in the program. The connections are a list of list of connection information. We can see that there is one group connecting left and right with rails, and another group that connects up and down with roads.
Tile( "overpass", [ [ (Direction.LEFT, TransportType.RAIL), (Direction.RIGHT, TransportType.RAIL) ], [(Direction.UP, TransportType.ROAD), (Direction.DOWN, TransportType.ROAD)] ] )
The “T rail station” connects them in just one group and mixes the transport type. The tile looks like this:
And then the code features only one connectivity group with three elements:
Tile( "T rail station", [ [ (Direction.LEFT, TransportType.RAIL), (Direction.RIGHT, TransportType.RAIL), (Direction.DOWN, TransportType.ROAD) ] ] )
The connectivity information is there, it just has to be used. And I can just start from each exit and see which other exists are reached when traversing the graph with backtracking.
Starting with tests
I will develop this with a test driven approach, just because it is so much fun. So we write the test first:
def test_empty() -> None: board = Board() clusters = get_cluster_sizes(board) assert clusters == []
This creates an empty board. It has 12 exits, but they are not connected to anything. So the list of cluster sizes is going to be an empty list. This test fails until I write a stub function:
def get_cluster_sizes(board: Board) -> List[int]: return []
Now the test works, and I can write the next test. This will put in one connection and see whether we get a cluster of size 2. The new test looks like this:
def test_single_connection() -> None: board = Board() straight_rail = Tile( "straight rail", [[(Direction.LEFT, TransportType.RAIL), (Direction.RIGHT, TransportType.RAIL)]], ) for j in range(1, board.board_size - 1): board.board[2][j] = straight_rail make_board_image(board, "test_single_connection.png") clusters = get_cluster_sizes(board) assert clusters == [2]
The board that generates is this one:
We can see that it should connect the two exits. We expect that there is a single cluster with two exists, hence the expected result of [2]. For this test we really need to write the body of the function now.
Backtracking
For backtracking it is crucial that we remember where we have been. My first idea has been to just track the lattice sites. But that doesn't quite suffice when we have the “double road” tile:
In that case, just with the overpass, we can actually traverse the same tile twice, as long as we are on the different connectivity cluster within the tile. So that means that we not only have to keep track of the tiles, but also which part of the tiles we have been.
Getting the cluster sizes is now rather straightforward. We just let it iterate from every exit, see how many other exists we can reach. Reached exists are not searched again. We then take the number of other exists reached as the size.
def get_cluster_sizes(board: Board) -> List[int]: found_connections = {} for exit_position in exit_positions: # There is no point in performing a search if the current source is already a # target with a different cluster. if any(exit_position in targets for targets in found_connections.values()): continue iterator = ConnectivityIterator(board, exit_position + (0,)) observer = ConnectivityObserver() backtracking = Backtracking(observer) backtracking.run(iterator) found_connections[exit_position] = observer.exits sizes = [len(targets) for targets in found_connections.values() if len(targets) > 1] sizes.sort(reverse=True) return sizes
But then we need to have the matching observer and iterator to use the backtracking algorithm. The iterator contains the necessary logic to go to the next tiles which are connected via the same local connection that we are already on. We track the positions and connection indices in visited to make sure that we don't cross on our selves.
class ConnectivityIterator(TreeIterator): def __init__( self, board: Board, pos: Tuple[int, int, int], visited: List[Tuple[int, int, int]] = [], ): self.board = board self.pos = pos self.visited = visited def get_children(self) -> Generator["ConnectivityIterator", None, None]: i, j, connection_idx = self.pos current_tile = self.board.board[i][j] assert current_tile is not None current_connection_cluster = current_tile.connections[connection_idx] for direction, transport_type in current_connection_cluster: ii, jj = direction_to_coordinates(i, j, direction) next_tile = self.board.board[ii][jj] if next_tile is None: continue for next_connection_idx, next_connection_cluster in enumerate( next_tile.connections ): for next_direction, next_transport_type in next_connection_cluster: if opposite_directions[next_direction] == direction: new_pos = (ii, jj, next_connection_idx) if new_pos in self.visited: continue yield ConnectivityIterator( self.board, new_pos, self.visited + [self.pos] )
The observer just tracks the exists that we have visited.
class ConnectivityObserver(Observer): def __init__(self): self.exits = set() def observe(self, state: ConnectivityIterator) -> None: i, j, connection_idx = state.pos if (i, j) in exit_positions: self.exits.add((i, j))
I use a set such that start and end are not counted multiple times.
Evaluation of connectivity
I have just let the random walk run through and then looked at the connectivity in each step. Whenever there was a transition, I have generated an image.
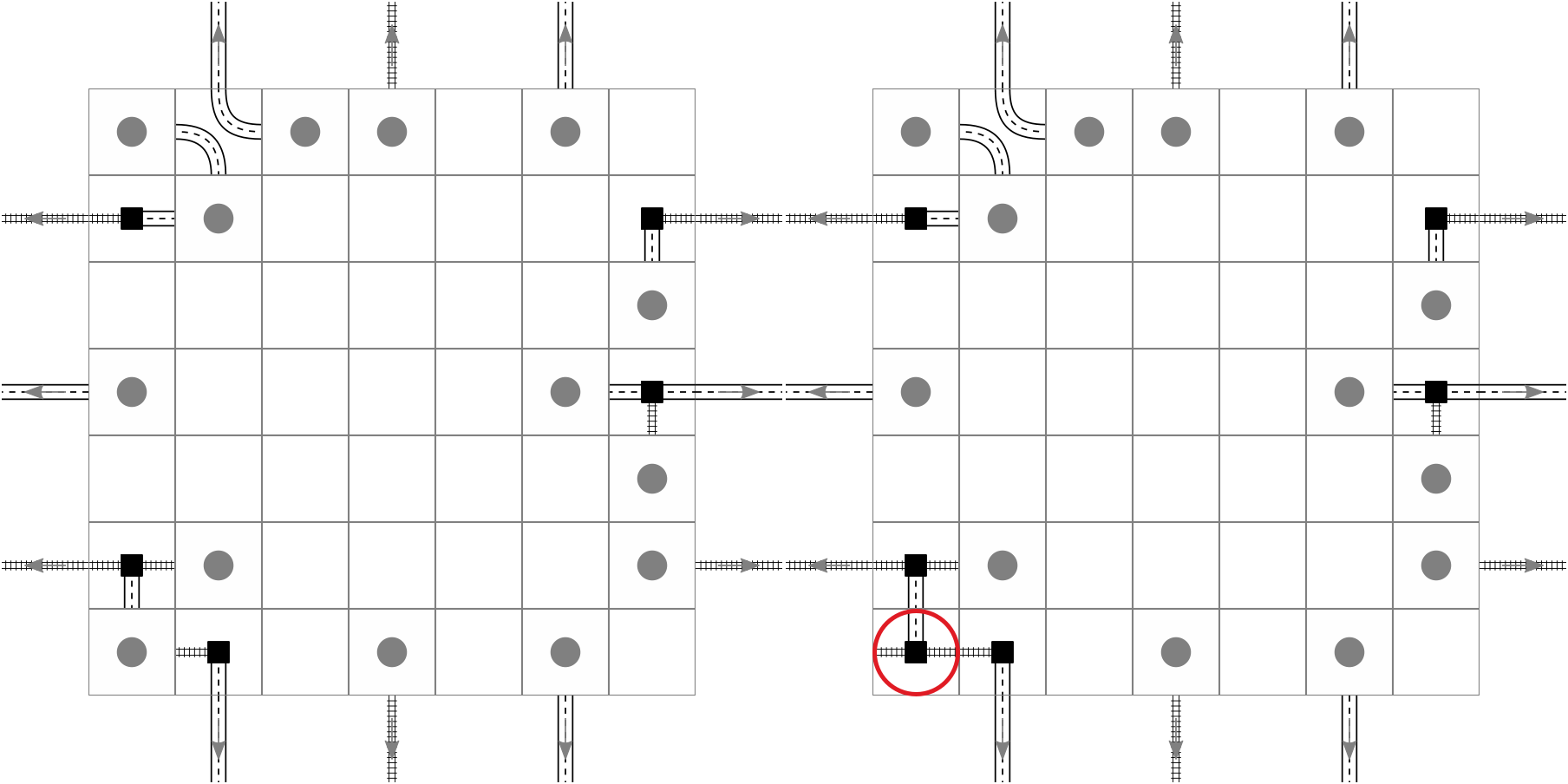
In the following image we have the transition from no connectivity to a single cluster with two exists, denoted as (2). The left picture is before, and in the right one new element has been added.
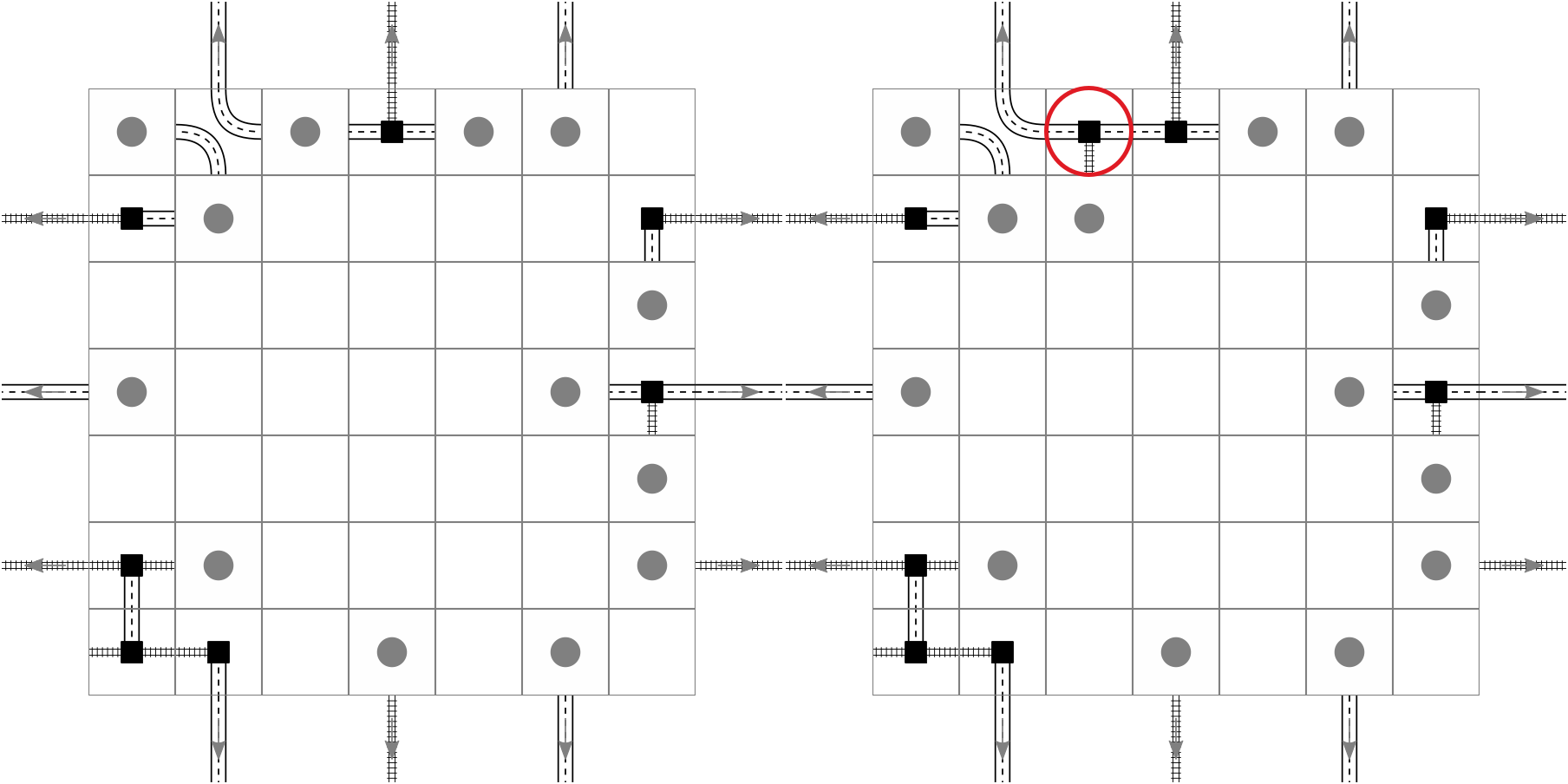
Then in the next transition we go from (2) to (2, 2):
We eventually go from (2, 2) to (3, 2) when another gap is closed:
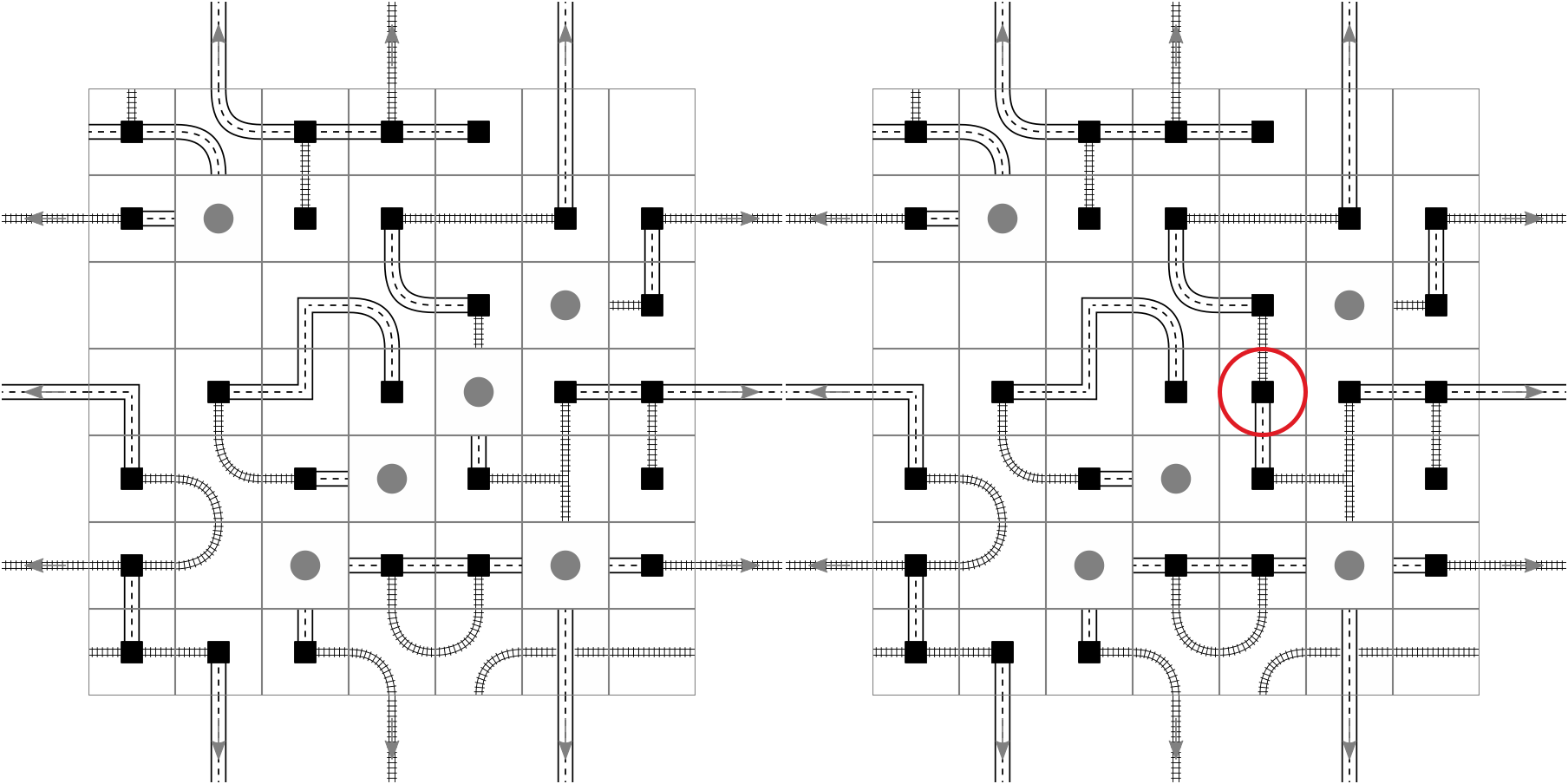
And towards the end we go from (3, 2) to (3, 2, 2):
This seems to work, although it is not clear whether the double layer really works. I didn't need to use an external library but could reuse some of my code, which feels great.
Running Monte Carlo tree search
With all that in place, adding the scoring for the MCTS was just utterly simple:
class ClusterSizeBackpropagation(MCTSBackpropagation): def get_win_score( self, it: TreeIterator, start_players_turn: bool ) -> Union[int, float]: assert isinstance(it, RailroadInkIterator) cluster_sizes = get_cluster_sizes(it.board) if cluster_sizes: return cluster_sizes[0] / 12 else: return 0
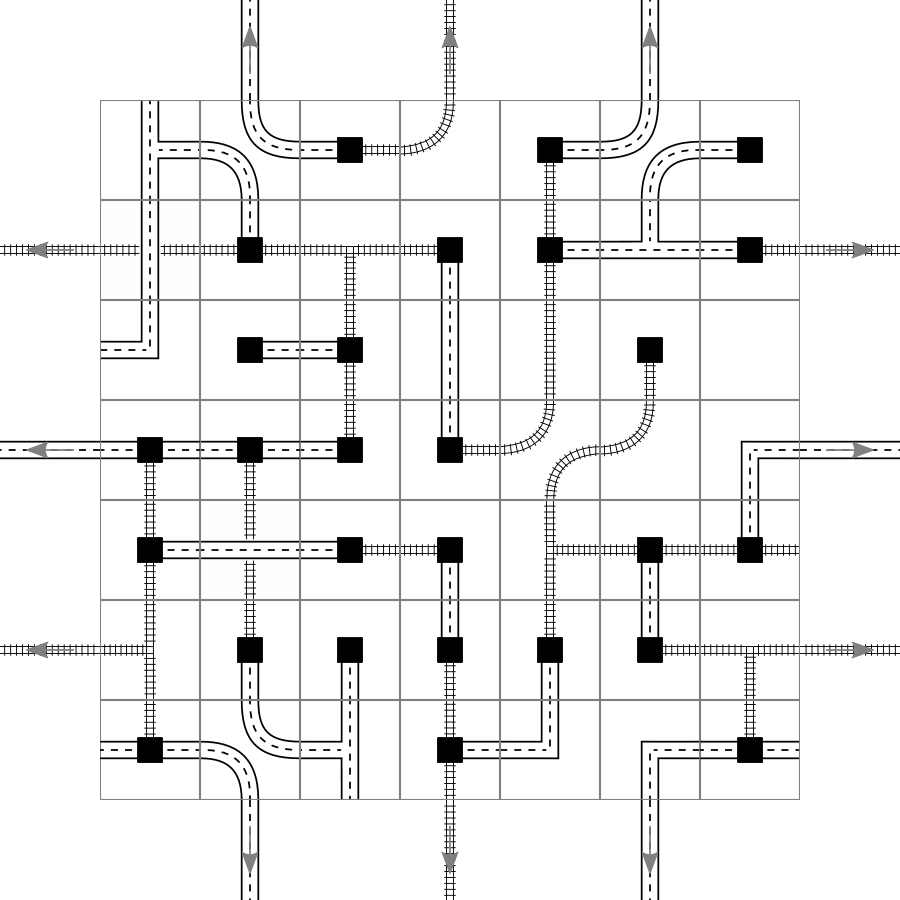
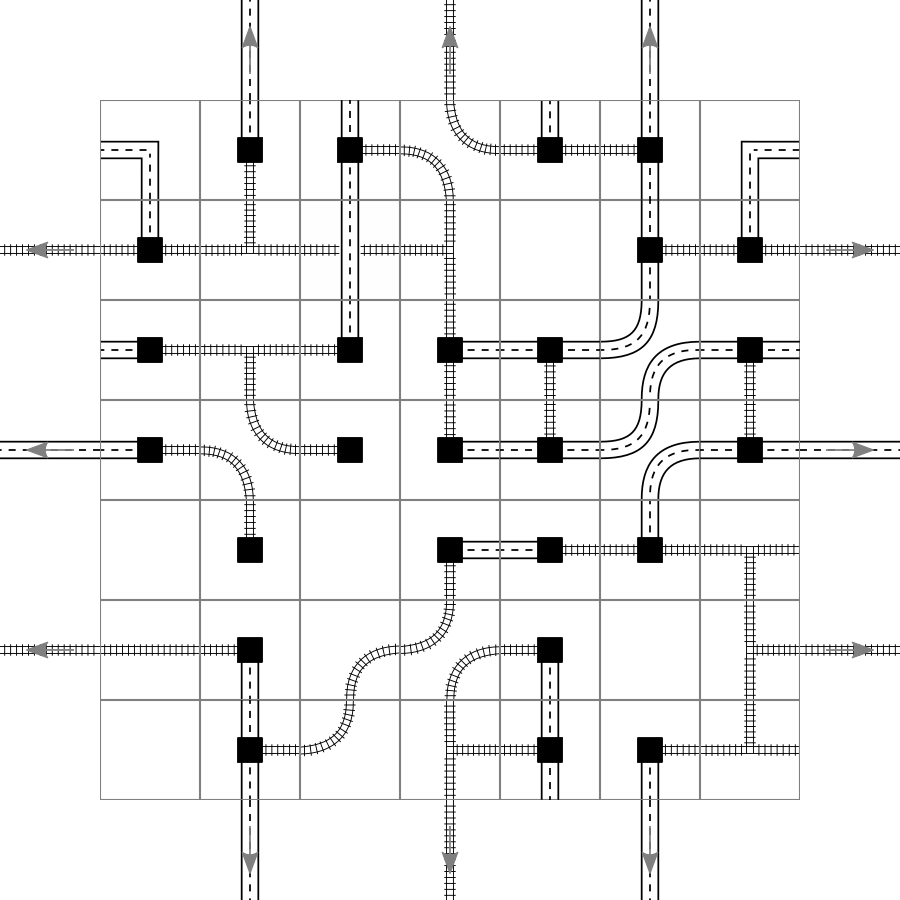
And with that I could let it run. It made around 500 steps before it filled up 4 GB of memory. So likely I would need to make it more efficient, dump branches or something like that. While it was searching, it found a couple of interesting configuration. The one with the largest cluster with configuration 117 with (10, 2):
I find that this one looks very pleasing. Also it shows that the curves are correctly resolved and that the exits are counted correctly.
And then later configuration 252 also got a (10). But that one doesn't have the other two exists connected to each other, so it is not as nice.
Conclusion
This again was pretty fun. I really love the images that come out, they look rather pretty compared to what I usually get.
The MCTS was not really successful here. I don't have enough memory to keep it running for long. We have seen that the number of configurations is absurdely high, and I was able to run fewer playouts than with Tic-Tac-Toe. So I would think that this game needs much more computing power and more cleverness in the algorithm. This is not that surprising as board games are scaled in complexity such that they are complicated enough to be fun and that one cannot plan out ahead everything.
Maybe in the future I will fine some more simple problems where I can apply the MCTS.