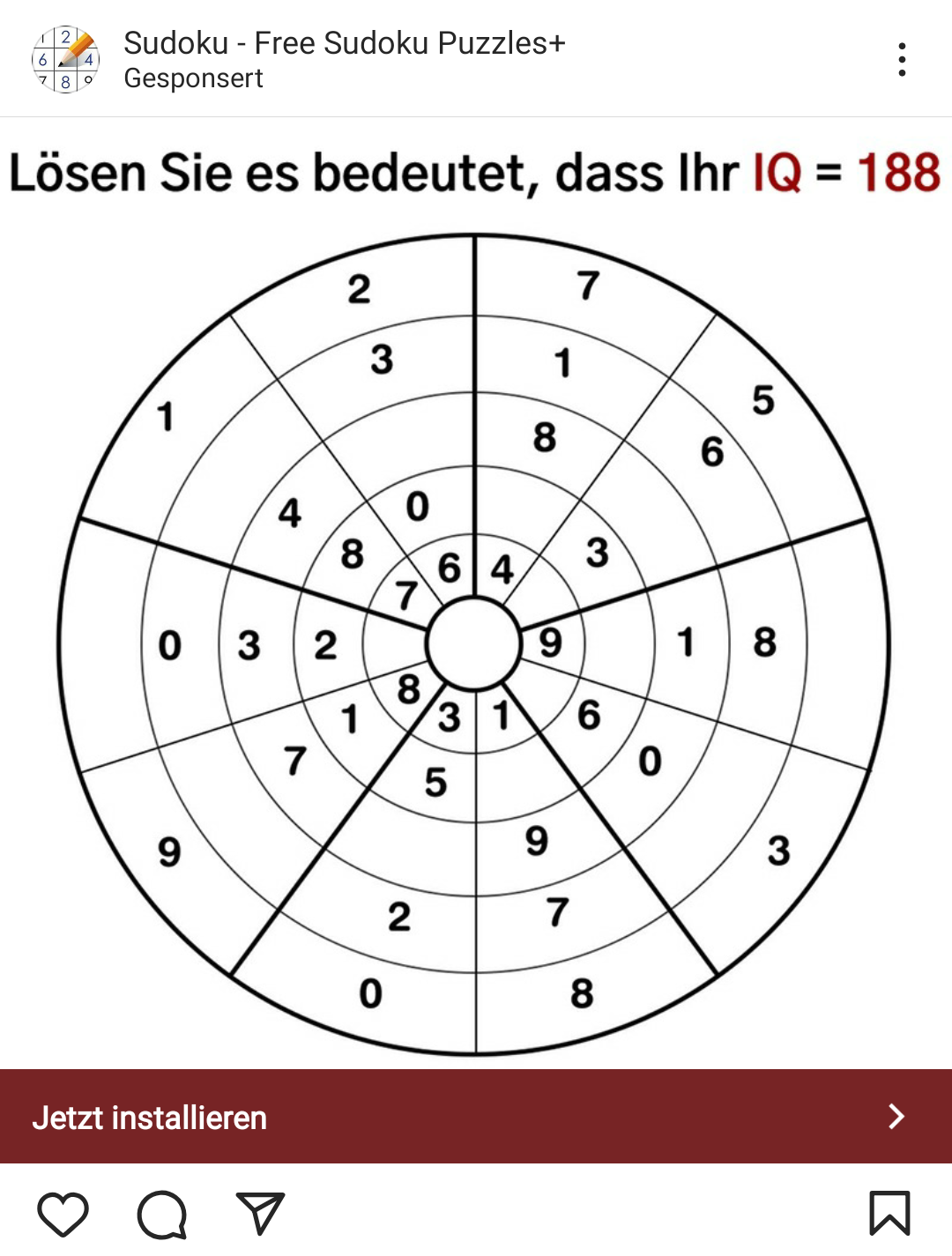
Rundes Sudoku

Martin Ueding

2022-07-16

Code & Zahlen

In sozialen Netzwerken findet man häufig Werbung, die reines Clickbait ist. Es geht gar nicht darum, ein gutes Produkt anzupreisen, sondern Leuten durch psychologische Tricks das Geld aus der Tasche zu ziehen. Hier ist es eine Werbung für eine Sudoku-App. Sie hat war Free im Namen, wird aber bestimmt In-App-Käufe haben. Vielleicht kann man sich Tipps kaufen, wenn man nicht mehr weiterkommt, ich habe es nicht angeschaut.

Hier in der Werbung wird versucht mit Scham zu arbeiten: »Wer das nicht lösen kann, ist dumm.« Vor allem ist ein IQ von 188 ein abartig hoher Wert, das bringt auch seine Nachteile mit sich. Ob das jetzt so erstrebenswert ist, weiß ich nicht.

Ich springe auf solche Werbung an, aber aus anderen Gründen. Ich finde sie zum einen psychologisch interessant, zum anderen ist es ein durchaus spannendes Problem, zu dem ich einen Blogeintrag schreiben kann. Ich möchte also hier zeigen, wie man ein Programm schreiben kann, das dieses Rätsel löst.

Für dieses Problem werde ich Python nutzen, das wird hoffentlich schnell genug sein.

Darstellung des Rätsels

- [2, 3, null, 0, 6]
- [1, null, 4, 8, 7]
- [null, 0, 3, 2, null]
- [9, null, 7, 1, 8]
- [0, 2, null, 5, 3]
- [8, 7, 9, null, 1]
- [3, null, 0, 6, null]
- [null, 8, 1, null, 9]
- [5, 6, null, 3, null]
- [7, 1, 8, null, 4]

Dann brauchen wir noch eine Funktion, mit der wir das ganze schön darstellen können. Hier nehme ich Matplotlib:

def make_image(data):
    angle_correction = -2.5/10 * 2*np.pi

    pl.clf()
    pl.gcf().set_size_inches((5, 5))

    for i in range(1, 7):
        r = np.ones(100) * i
        phi = np.linspace(0, 2 * np.pi, 100)
        x = r * np.cos(phi)
        y = r * np.sin(phi)
        pl.plot(x, y, color='black')

    for phi in np.linspace(0, 2 * np.pi, 11) - angle_correction:
        r = np.linspace(1, 6, 3)
        x = r * np.cos(phi)
        y = r * np.sin(phi)
        pl.plot(x, y, color='black')

    for i, row in enumerate(data):
        for j, cell in enumerate(row):
            if cell is None:
                continue
            r = (4-j) + 1.5
            phi = (2*np.pi) / 10 * (i + 0.5) - angle_correction
            x = r * np.cos(phi)
            y = r * np.sin(phi)
            pl.gca().annotate(str(cell),  xy=(x-0.2, y-0.2))

    pl.gca().set_axis_off()

make_image(data)
pl.savefig('init.svg', dpi=150, bbox_inches='tight')
pl.show()

So erhalten wir eine SVG-Grafik des Anfangszustandes:

Nun können wir uns Algorithmen anschauen, die eine Lösung dafür erzeugen. Wir müssen noch eine Maske ableiten, in der die veränderlichen Felder stehen:

mask = [(i, j) for i, row in enumerate(data) for j, cell in enumerate(row) if cell is None]

Das ist dann eine Liste von Sektor- und Radiusindizes, die veränderlich sind.

Backtracking

Als erstes ist Backtracking eine gute Wahl. Damit hatte ich schon andere Clickbait-Werbung zerstört, und Lösungen für Railroad Ink erzeugt. Der Algorithmus ist relativ einfach. Wir füllen einfach überall die erstbeste Zahl ein, bis wir uns in eine Sackgasse manövriert haben. Dann gehen wir einfach so lange zurück, bis wir wieder neue Optionen. Das macht man so lange, bis man eine Lösung es Problems gefunden hat.

So sieht der Algorithmus in rekursiver Implementierung aus:

# Liste für erreichte Lösungen.
solutions = []
# Iterationszähler für Video-Export
iteration = 0

def backtrack(mask_idx):
    # Exportiere den aktuellen Stand als Bild.
    global iteration
    make_image(data)
    pl.savefig(f'{iteration:010d}.png', dpi=150, bbox_inches='tight')
    iteration += 1

    # Falls wir am Ende der Maske angekommen sind, haben wir eine Lösung gefunden!
    if mask_idx == len(mask):
        solutions.append(copy.deepcopy(data))
        return

    # Wir holen uns die Position, die wir füllen sollen.
    i, j = mask[mask_idx]

    # Dann gehen wir alle Ziffern durch:
    for c in range(10):
        # Wir müssen prüfen, ob die Ziffer einmal im Ring ist:
        ring = [row[j] for row in data]
        # Falls der Kandidat schon im Ring ist, überpringen wir.
        if c in ring:
            continue
        # Wir prüfen den einen Radius:
        if c in data[i]:
            continue
        # Und den gegenüberliegenden Radius:
        if c in data[(i + 5) % 10]:
            continue

        # Die Ziffer kommt noch nicht vor. Wir setzen sie rein.
        data[i][j] = c
        # Und nun füllen wir noch die restlichen Felder..
        backtrack(mask_idx + 1)

    # Auf dem Rückweg leeren wir wieder das Feld.
    data[i][j] = None

    make_image(data)
    pl.savefig(f'{iteration:010d}.png', dpi=150, bbox_inches='tight')
    iteration += 1

# Start der Rekursion.
backtrack(0)

Das Programm liefert vier Lösungen, das Sudoku ist also nicht eindeutig lösbar, sondern unterbestimmt. Das macht es noch etwas schwerer. Dies sind die vier Lösungen:

Der Algorithmus hat keine 100 Schritte gebraucht. Diese können wir hier sehen:

Es sind also schon ziemlich viele Zahlen enthalten, sodass gar nicht mehr so viel zu tun ist. Der Algorithmus kommt auch immer direkt bis zum Ende. Wenn man also greedy einfach irgendwo anfängt und Zahlen einsetzt, die noch verfügbar sind, kommt man direkt auf eine Lösung.

Händische Lösung

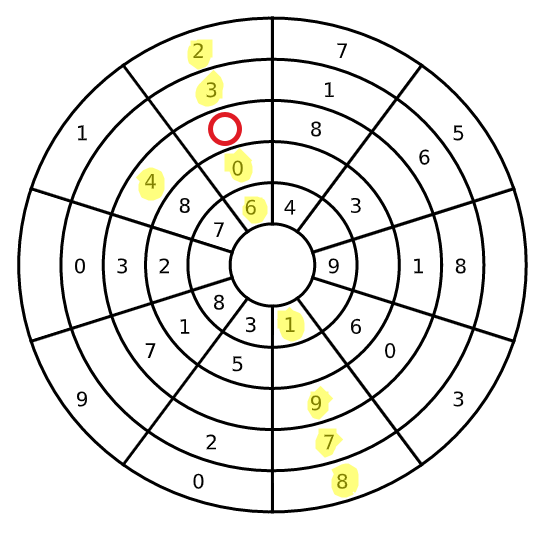
Also letztlich ist es ein Sudoku, das wirklich extrem platt ist. Schaut man sich die erste Lücke an, so kann man direkt alle Zahlen außer der 5 ausschließen:

Und bei der zweiten Lücke kann man alle Zahlen bis auf 5 und 9 ausschließen:

Man muss also nur zwei Möglichkeiten weiterverfolgen. Beide führen zu einer validen Lösung, man kommt also noch nicht einmal in eine Sackgasse. Dieses Sudoku löst jemand mit Regelkenntnis in wenigen Minuten. Dafür einen IQ von 188 auszuloben, erscheint mir doch etwas übertrieben.

SAT-Solver

Das ganze kann man auch mit einem SAT-Solver machen. Dazu muss man die Abhängigkeiten entsprechend in der Sprache des SAT-Solvers ausdrücken. In diesen Vorlesungsnotizen wird das für ein normales rechteckiges Sudoku einmal vorgeführt.

Fazit

Sudokus sind eigentlich sehr spannende Probleme. Das hier war sehr öde. Und dann auch noch mit dieser Clickbait-Werbung, die auf Scham zielt, ist es auch noch moralisch verwerflich. Aber immerhin eine weitere Gelegenheit mit Backtracking herumzuspielen und ein lustiges GIF zu erzeugen.