Simulating Scythe: Greedy Beam Search
Scythe is a board game from the engine builder genre. Is a rather complicated game as there are different types of entities and actions around. It is about collecting resources, deploying the hero, workers, mechs and buildings, moving them around, fighting with others, accomplishing achievements. In the end one obtains a score based on the number of achievements, controlled hexes and resources as well as left-over money and some bonus points.
The player will pick a random player mat, the following shows the innovative mat (German version):
Every turn one picks a new column and performs the top, bottom or both actions. There are certain patterns that lead to successful game play. Most importantly one should strive to do both the top and bottom action in order to get the most done each turn. With the innovative board, the bolster action is combined with the build action. Therefore one should have some wood ready when picking this to perform both actions. But wood is collected either through the trade or produce top-row actions, which have their own bottom-row actions. Different player mats have different arrangements, therefore the cycles that one goes through are also different. After playing this game a couple of times, one gets better at building a good engine.
Whenever I play such games, I see a game graph in my head. Abstract models seem to be more present than the beautiful artwork of the game. So I spend a whole rainy Saturday actually implementing a subset of the game and let if figure out good ways to build that engine. In this blog post I want to share the code, explain my approach and share some results. There is so much more to be done, but there is only so much one can do in one sitting.
Complexity assessment
Simulating the whole game likely is going to be too complicated for a start, so instead I wanted to see whether there are certain starting patterns that give a good start. In order to make it a bit simpler, I start with just one nation (Togawa Shogunate) that has all resources accessible without needing to deploy a mech. In this way I can pretend that the game has just five hexes and still collect the four types of resources and deploy more workers. Also I will assume that the player is not attacked by other players.
In an abstract way, the actions of the considered player will form a directed graph. There is a starting node which is set by the player mat and faction mat. From there different actions are possible, I would estimate that there are up to around 20 options in each round. A typical game lasts around 20 to 30 rounds, so the complexity of the graph might be 1,073,741,824,000,000,000,000,000,000,000,000,000,000 edges. Building the whole graph is completely out of the question. One cannot always do everything in every round, a lack of resources for instance means that a certain action cannot be done. Still, the number likely remains large. Strategies to cope with that complexity are needed.
The approaches that I see are these:
-
Just simulating a few steps in full, such that the total complexity remains manageable. Only the actions that are valid will be done, so perhaps one can do it a few steps. The graph will have full breadth, but the depth will likely be too short to really see anything useful.
-
Using plain random sampling will effectively be a random walk. One can therefore sample to the end of the game (reaching six achievements), but the trajectories will likely be completely useless. Also it might take ages to actually terminate as it might just cluelessly move around, collect resources but not invest them.
-
Do something like a beam search and only keep the most promising candidates. In this way one can control the complexity, keep a fixed width and simulate to the end of each game. One just needs to find some measure to rank the beams.
-
Use a policy learning algorithm to actually learn the game and make good decisions. These could be genetic algorithms or deep learning with reinforcement learning.
At the moment I think about option 3, but first I will have to implement a representation of the game. Once I have it, I can also do option 1 and 2 to get started.
Representation framework
The graph needs to be represented somehow.
-
One can have fat nodes which represent the state of the game. The edges are then just simple connections. One can recover the step by taking the difference between states, but that is not necessarily unique.
-
Or the nodes are simple and the edges contain details about the move. This way one would have to track the state along the edges, but would not have to store it.
-
Just do both. The state needs to be formed anyway, it makes sense to store it. And the moves need to be formed, so they could be stored as well.
I therefore need something to represent the state of the game and also represent the moves. I want it to be rather general and am thinking towards a polymorphic thing with States and Moves in between them.
State
The game has a lot of state:
- Locations of hero, mechs and workers. The location might be on the player mat, the home circle or any of the hexes in the game.
- Last column that the player selected on the player mat. Most factions cannot perform the same action twice.
- Locations of resources. This can be simplified by just counting the total resources as in this simplified setup there is no reason for them to get inaccessible anyway.
- Popularity points.
- Power points.
- Money.
- Locations of the buildings, can be on the player mat or any of the hexes.
- Status of the upgrades, this modifies the actions that are possible. Upgrades to the top and bottom row are somewhat independent, they can be done in arbitrary pairs.
- Depending on the deployed mechs there are different modifiers for battle and movement. The Togawa Shogunate faction is simpler as the movement modifiers don't change so much and that I can ignore them for the start.
- The achievements. Some can be derived from others, like having all workers, all mechs, all recruits, all buildings, all upgrades. But having had full popularity or full power once are not persistent in the state and need to be tracked.
- Number of combat cards and their values. I'll just count their number.
- Encounters that are done (I'll ignore that here).
I want the state to be easy to copy, so it should just be a simple Python dictionary. This way I can also just use JSON.
Moves
Each round works like this:
- Select a different column from the player mat.
- On the top, choose whether you want to do the action, the alternative (if available) or nothing. Upgrades might allow doing more (producing on a third hex, moving three entities, getting two coins, getting three power, getting two combat cards, getting two popularity). Buildings may also give more (popularity, power, production).
- On the bottom, choose whether you want to perform that action. Upgrades might have reduced the cost. Recruits might have given additional bonuses.
- Check whether you have triggered any achievements.
Each player mat has a different arrangement of top and bottom row actions. Also the costs for the bottom row actions are different.
The moves must be more complicated than the state. I think of a polymorphic structure for top-row and bottom-row actions. They can take the state to see whether they can do that. And then they output possible final states that could come out of that. This way every action can have arbitrary logic without interfering with others.
The player mat will then be just a list (for the columns) with tuples (for top and bottom). The state will be a simple dict. And the actions will be simple stateless functions that take a state and return a list of states. In the main loop I just need to go over all actions and combine the states that come out. A scoring function can compute a number for the given state.
The state will contain a list with string representations of the last actions such that every state has a human understandable sequence of steps attached to it. This way a player can just realize some outcome in the game.
Board
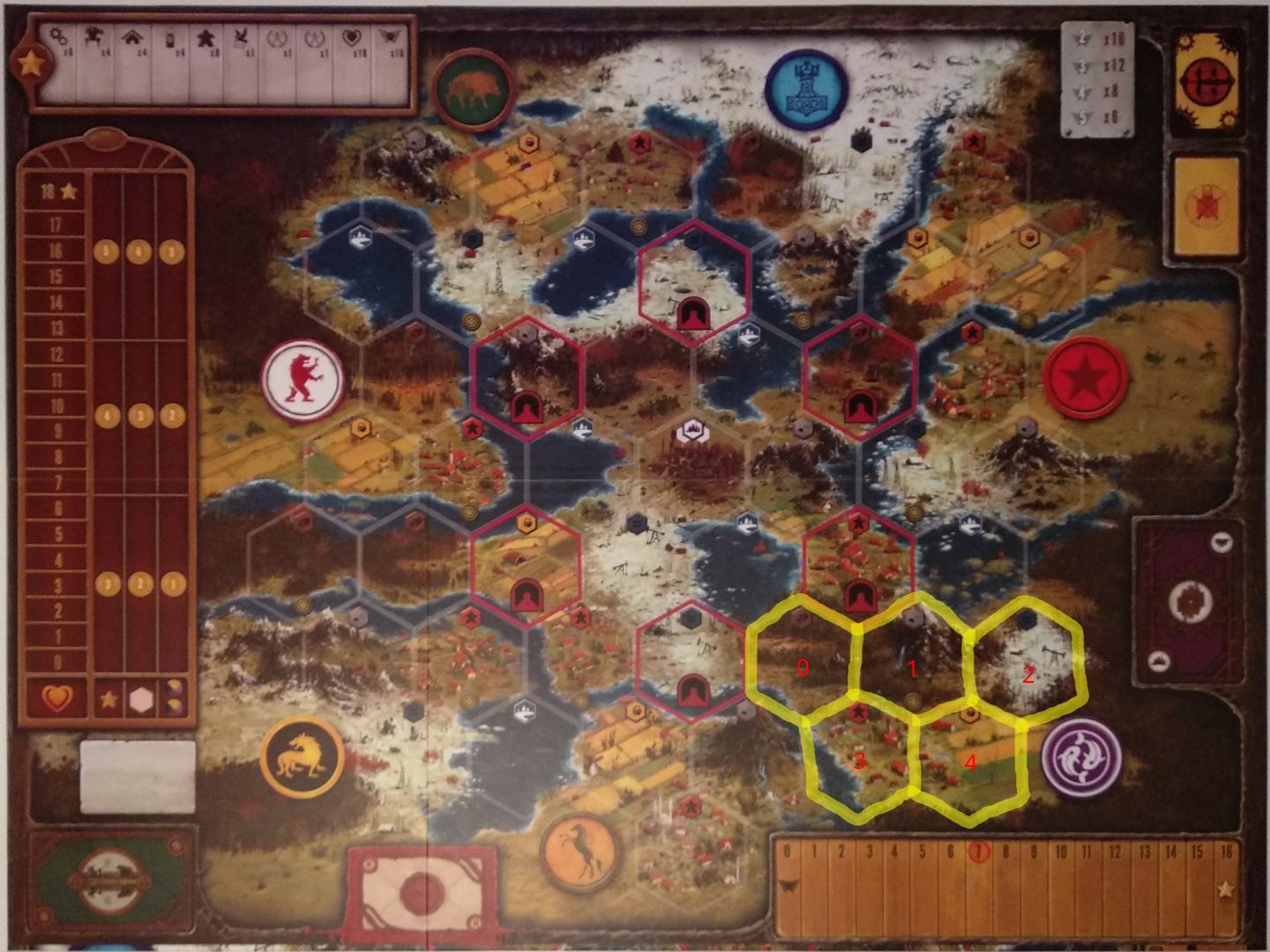
The board is rather large, and what I really need are the next neighbor relations only. Then the move action can go and traverse the board. I only simulate the closest five hexes near the purple starting marker in the lower right. This way I have one hex with grain, metal, oil and wood, as well as a village to spawn more workers.
Implementation
Because this is a hobby project and performance would be nice, but I want to get some results quickly, I choose Python. Also I wanted to implement my own tree data structure, my own beam search. Surely there are libraries for game simulation, and I know a few graph libraries. Still I just want to implement everything on my own as learning project. In a production environment I would recommend to use tested libraries, though.
The tree/graph of states is really simple. It just has nodes, and every node has a parent and multiple children. I have decided to not label the edges at all, rather the state will have an attribute actions that is a list with sentences describing the actions taken so far. This way the state has a history and one can also just take any state and continue the simulation from it.
The starting state is shown in the following. We don't have any achievements yet. We haven't performed any actions. There are no buildings built. We have two combat cards. There are no resources collected yet. The hero is on hex 5, the board will be shown shortly. The last action we did is -1 such that in the first move we are free to do any of the four. We haven't deployed any mechs yet. We start with 5 coins, 3 popularity and 0 power. There are no recruits yet. Also we don't have any upgrades on the top and bottom. And two workers are out on hexes 2 and 4.
{'achievements': [], 'actions': [], 'buildings': {}, 'combat cards': 2, 'grain': 0, 'hero': 5, 'last column': -1, 'mechs': [], 'metal': 0, 'money': 5, 'oil': 0, 'popularity': 3, 'power': 0, 'recruits': {}, 'upgrades bottom': {'build': 0, 'deploy': 0, 'enlist': 0, 'upgrade': 0}, 'upgrades top': [], 'wood': 0, 'workers': [2, 4]}
The board is just a list of hexes with the neighbor numbers. This is a bit tedious, but okay for the start.
Hex = collections.namedtuple('Hex', ['type', 'neighbors']) board = [ Hex('wood', [1, 3]), Hex('metal', [0, 2, 3, 4]), Hex('oil', [1, 4]), Hex('workers', [0, 1, 4]), Hex('grain', [1, 2, 3]), Hex('home', [2, 4]), ]
The actions are simple functions that take a state (dict) and emit a list of possible resulting states. The trade action is perhaps the simplest, as we can either buy any of two resources or buy popularity. The amount of popularity is increased with the upgrade. We see the construction of all possible states here:
def trade(state: dict) -> typing.List[dict]: # We need to pay one money. if state['money'] == 0: return [] state = copy.deepcopy(state) state['money'] -= 1 if 'armory' in state['buildings']: increase_power(state, 1) final_states = [] # We can choose to buy any two resources. types = ['grain', 'metal', 'oil', 'wood'] for i, res_1 in enumerate(types): for res_2 in types[i:]: state_resource = copy.deepcopy(state) state_resource[res_1] += 1 state_resource[res_2] += 1 state_resource['actions'][-1][0] = 'Buy {} and {}'.format(res_1, res_2) final_states.append(state_resource) # Alternatively we can invest into our popularity state_popularity = copy.deepcopy(state) amount = 1 if 'popularity' in state_popularity['upgrades top']: amount += 1 increase_popularity(state_popularity, amount) state_popularity['actions'][-1][0] = 'Buy popularity' return final_states + [state_popularity]
I have similar functions for all top-row and bottom-row actions. The player mat is then constructed from these actions. For the other actions I need to specify the base cost, upgradable cost, and the monetary reward. Having these in an unnamed tuple is not the nicest, but I can refactor that later on.
mats = {'innovative': PlayerMat( actions=[ (actions.trade, actions.upgrade), (actions.produce, actions.deploy), (actions.bolster, actions.build), (actions.move, actions.enlist), ], upgrade=(3, 0, 3), deploy=(2, 1, 1), build=(3, 1, 2), enlist=(1, 2, 0), ) }
Then I have a main loop, which takes all the leaves in the tree from the previous step. It goes through every of these states and chooses all three available columns from the player mat. Then it either does the top-action, bottom-action or both. The resulting states are collected as the children.
This quickly spirals out of control. We start with 1 state. After the first iteration we are already at 34 possible states. We then have 556 (an increase by factor 16.4), and then 15089 (factor 27.1). This is point where a full breadth search doesn't work any more. Some more clever graph search algorithm is needed.
Beam search
I chose to implement the beam search first. This means that I take only the top candidates and compute the next turn for these. The choice of beams is critical here. In my first approach I just ranked them by the total end score in the game. Taking the top 500 states, I would continue with the computation.
Scoring by final score is really short-sighted and the system will select the moves in this fashion. The best strategy then is to produce grain and oil with the starting workers, buy two more oil, and do the upgrade to get two coins in that top-action. Then it will just alternatively get money (two final points) and produce (two resources mean 1 point). Performing another upgrade just costs resources which will be reflected in the final score only much later. Buying popularity would increase the total score from the resources, but because beams with short-term benefits are chosen, these long-term strategies are eventually dropped from the search.
I needed to have a better judgment whether a strategy should be pursued further. Instead of going by final points, I have scored each beam by the number of workers/upgrades/buildings/recruits/mechs squared. This way it is incentivised to finish all of one type to get an achievement. I scored achievements really strongly, but that then dropped out all beams which would have had an achievement just one step later.
In order to still allow some long-term beams survive, I have not only taken the top 1500 best scored beams, but another 500 randomly sampled from the other ones. This is not really a good strategy as it isn't reproducible.
After 25 steps, the top candidate that I have is the following with a score of 60. One should make clear that the search hasn't planned anything. It just happened to be the most successful alternative that has survived. It has produced all upgrades, which makes sense with the innovative board as the reward is the highest. It has also started upgrading the upgrade action first such that this became cheaper.
{'achievements': ['all upgrades', 'all buildings', 'all recruits'], 'actions': [['Produce 1 oil on H2 and 1 grain on H4', None], ['Buy oil and oil', 'Upgrade money and upgrade'], ['Produce 1 oil on H2 and 1 grain on H4', None], ['Buy grain and oil', 'Upgrade production and upgrade'], ['Get money', 'Enlist deploy for money'], ['Buy grain and oil', 'Upgrade movement and upgrade'], ['Get money', None], ['Buy grain and grain', 'Upgrade popularity and build'], ['Get money', 'Enlist build for popularity'], ['Buy wood and wood', 'Upgrade power and build'], [None, 'Build armory on H2'], ['Buy wood and wood', 'Upgrade combat cards and deploy'], [None, 'Build tunnel on H4'], ['Move, worker from 2 to 1, worker from 4 to 3', None], ['Buy wood and wood', None], [None, 'Build monument on H3'], ['Buy wood and wood', None], [None, 'Build mill on H1'], ['Buy grain and grain', None], ['Move, worker from 1 to 0', None], ['Buy grain and grain', None], ['Get money', 'Enlist enlist for power'], ['Buy grain and grain', None], ['Get money', 'Enlist upgrade for combat cards'], ['Buy grain and grain', None]], 'buildings': {'armory': 2, 'mill': 1, 'monument': 3, 'tunnel': 4}, 'combat cards': 5, 'grain': 2, 'hero': 5, 'last column': 0, 'mechs': [], 'metal': 0, 'money': 31, 'oil': 0, 'player mat': 'innovative', 'popularity': 9, 'power': 9, 'recruits': {'build': 'popularity', 'deploy': 'money', 'enlist': 'power', 'upgrade': 'combat cards'}, 'score': 60, 'score search': 372, 'upgrades bottom': {'build': 2, 'deploy': 1, 'enlist': 0, 'upgrade': 3}, 'upgrades top': ['money', 'production', 'movement', 'popularity', 'power', 'combat cards'], 'wood': 0, 'workers': [0, 3]}
There are some clear playing mistakes:
- It has enlisted the deploy-recruit first, although it never deployed any mechs. Rather it did an upgrade right after, so having the upgrade-recruit first would have given more power.
- It has also moded a worker from hex 1 to hex 0 but didn't do anything with it. Just getting money would have been better.
- There are rounds where it just buys wood but doesn't do a bottom-action. And then it just does the build action without bolstering. If it would either bolster or buy popularity, it would eventually get an achievement. Also it would have higher scores for the everything else.
Other mistakes are also possible, and I have tried to drop beams where such mistakes are visible. For instance I don't want it to collect resources which cannot be spent. Say if all mechs are deployed, there is no point in having more metal, although the resources give more points.
Worker production
Having specific goals might be better. I could for instance want to have the most workers and then the most mechs in the first couple of rounds. So I give 5 points for the first mech and 10 points for the first worker. Nothing else is incentiviced. Building additional ones from the one started gives extra points such that the achivement will be unlocked. The scoring will then simply this:
score = 0 score += 5 * len(state['mechs'])**2 score += 10 * len(state['workers'])**2
The problem with this is that a lot of beams get the exact same score. By also adding the regular score back to the mix, we can see that the system produces more workers, but also distributes them on the hexes such that it can get the largest score from area control.
{'achievements': [], 'actions': [['Move, worker from 4 to 3', None], ['Produce 1 oil on H2 and 1 workers on H3', None], ['Buy oil and oil', 'Upgrade movement and deploy'], ['Produce 1 oil on H2 and 2 workers on H3', None], ['Move, worker from 3 to 0, worker from 3 to 1, worker from 3 to ' '4', None], ['Buy oil and oil', 'Upgrade power and build']], 'buildings': {}, 'combat cards': 2, 'grain': 0, 'hero': 5, 'last column': 0, 'mechs': [], 'metal': 0, 'money': 9, 'oil': 0, 'player mat': 'innovative', 'popularity': 3, 'power': 0, 'recruits': {}, 'score': 19, 'score search': 269, 'upgrades bottom': {'build': 1, 'deploy': 1, 'enlist': 0, 'upgrade': 0}, 'upgrades top': ['movement', 'power'], 'wood': 0, 'workers': [0, 1, 2, 3, 4]}
But it doesn't produce more workers as for that it would require some power. And apparently all other actions give more points in the short term. Therefore there is a hindrance for it to first bolster and then produce some more workers.
Conclusion
This has been a fun weekend project, but the success is not that great. This was clear from the start, a game like this has extremely many options in each turn and without constraints it cannot sensibly produce a good run of the game. The greedy beam search showed ineffective to combat the complexity of the game and isolate better long-term strategies.