Simple Captcha with Deep Neural Network
The other day I had to fill in a captcha on some website. Most sites today use Google's reCAPTCHA. It shows little image tiles and asks you to classify them. They use this to train a neutral network to classify situations for autonomous driving. Writing a program to solve this captcha would require obscene amounts of data to train a neutral network. And if that would already exist, autonomous cars would be here already.
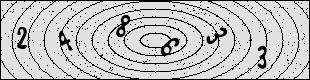
The captcha on that website, however, was of the old and simple kind:
It is just six numbers (and always six numbers), the concentric circles and some pepper noise. These kind of captchas are outdated because one can solve them with machine learning. And as I am currently working through “Deep Learning with Python” by François Chollet and was looking for a practise project, this captcha came as inspiration at just the right moment.
Obtaining data
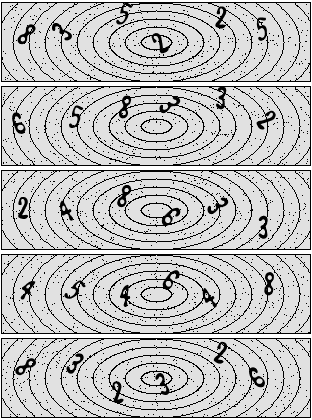
In order to do machine learning, one needs training data. I have downloaded a few of the captchas generated by the website. They look like this:
We could just download more and more captchas to use as training data. But then I would have to solve them all, and I do not want to do that. Instead, I'd rather build a very similar captcha generator and then just generate my training, validation and test data from that generator.
In order to generate, we need to observe how the captcha images are constructed. One can clearly see how the numbers always have almost the same $x$-location and the $y$-location is taken randomly. Also the numbers seem to have a random rotation applied to them.
Magnifying the “8” from the example shows that the digits are done with anti-alias, whereas the circles and the noise are not.
To generate something like this we can use the Pillow library. There we got drawing functions that can be used to generate such a captcha.
First we generate new image with the appropriate size and gray background. Also
we load some font and create a new ImageDraw object such that we can draw
onto the image.
image = Image.new('L', (310, 80), 221) font = ImageFont.truetype('Pillow/Tests/fonts/FreeSans.ttf', 27) d = ImageDraw.Draw(image)
Next we need do add the black border box that goes around the captcha.
d.line([0, 0, 309, 0], width=1) # Top d.line([0, 79, 309, 79], width=1) # Bottom d.line([309, 0, 309, 79], width=1) # Right d.line([0, 0, 0, 79], width=1) # Left
The ellipses are easy to measure in a program like GIMP. They have a spacing of 16 pixels in width and 8 pixels in height. Then we just need to increase the size of the bounding box and have a bunch of concentric ellipses.
for i in range(15): ellipse_width = 16 ellipse_height = 8 bbox = (image.width // 2 - i * ellipse_width, image.height // 2 - i * ellipse_height, image.width // 2 + i * ellipse_width, image.height // 2 + i * ellipse_height) d.ellipse(bbox, outline=0)
Next are the digits. When looking through many of the generated captchas one can see that there never are “1” or “7”. Also there never is a “9”, it is just “6”. That means that the list of digits is severely reduced and we just randomly pick out of that set. The $x$-locations I just read off from one of the sample captchas. Since I cannot find the exact font, it is not going to be pixel perfect either, so a slight shift in the locations does not hurt that much.
In order to rotate the digit I draw it onto a temporary image with alpha channel. Then I paste that onto the actual image.
allowed_digits = [2, 3, 4, 5, 6, 8] digits = [] for x in [17, 57, 115, 170, 217, 260]: txt = Image.new('LA', (20, 25), (150, 0)) dx = ImageDraw.Draw(txt) digit = random.choice(allowed_digits) digits.append(digit) dx.text((0, 0), str(digit), font=font, fill=(0, 255)) w = txt.rotate(random.uniform(-45, 45), expand=1) y = random.randint(14, 45) image.paste(w, (x, y), w.getchannel('A'))
For the pepper noise I just take 500 random points and make them black. I have tried 1000 points, but that was a bit too much.
for i in range(500): x = random.randint(0, 309) y = random.randint(0, 79) image.putpixel((x, y), 0)
In order to know which digits are actually contained in the file, I put them into the file name. And also a random number string such that I can have the exact combination multiple times without having to worry about clashes.
filename = '{}-{}.png'.format( ''.join(map(str, digits)), random.randint(1000, 9999)) image.save(filename)
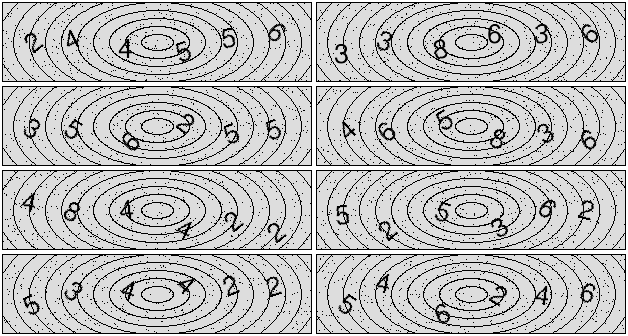
I think that the results look rather okay, although it is clear that the font is not exactly the same.
Using my script I can just generate as many of these as I want. I will just start with 2000 samples such that I have 1000 for training, 500 for validation and 500 for testing.
Preprocessing
We always have six digits in this captcha. One should always use available knowledge to make a numeric problem easier to solve. So we can just slice the captcha images into six slices and do a digit detection on each of them separately. I think that good slicing $x$-values are 54, 110, 170, 215, 262.
At this point I am not sure whether one should train one neural network per slice or use one neural network for all of them.
-
One network per slice means that it can fully learn the constant background of the ellipse and that it does not matter at all. So perhaps that would give us better accuracy.
-
If we are going for the latter, we would need to have something that works with different sizes. In this particular case we can just make the slices 51 pixels wide and just drop the gaps. Then the sizes are exactly the same.
But perhaps the neural network will have six times the input and learns to classify the digits better. The background would be a bit harder, because the neutral network would not know from which part of the image the slice came and therefore might have a harder time.
I just don't know in advance, so we will just have to find it out! The first option seems a bit easier to implement and test, so I will start that.
The loading of the image files can be done with the Pillow library or the Keras
wrapper keras.preprocessing.image.load_img. I have to convert the images to
grayscale and normalize them to fall into the interval $[0, 1]$. Then I take
the pixels up to column 54 such that I only look at the first digit with its
background. Additionally one needs to make sure that although they are
grayscale image, the dimensionality is still 3. The label needs to be in
one-hot-encoding. The following function takes a list of filenames and loads
them all.
def load_files(paths): images = [] labels = [] allowed_digits = [2, 3, 4, 5, 6, 8] for path in paths: image = keras.preprocessing.image.load_img(os.path.join('data', path)) grayscale = image.convert('L') array = np.asarray(grayscale) normalized = array / 255 images.append(np.atleast_3d(normalized[:, 0:54])) label = np.zeros(6) label[allowed_digits.index(int(path[0]))] = 1 labels.append(label) all_images = np.stack(images) all_labels = np.array(labels) return all_images, all_labels
I then use this function to load batches of the image files that I have generated before. The images are shuffled as the file names might be sorted and therefore the first digit would always be a “2”.
files = os.listdir('data') random.shuffle(files) train_images, train_labels = load_files(files[:1000]) validation_images, validation_labels = load_files(files[1000:1500]) test_images, test_labels = load_files(files[1500:2000])
Fitting the first digit
With the data in place we can now actually fit the first digit. I have taken a convolutional neutral network (convnet) from the book that detects local features via a convolution and then uses the pooling layer to gather information that is a bit less local. With four such blocks there is a factor $2^4 = 16$ in reduction that is scaled down. This network has been used for the binary classification of images of cats and dogs. So I presume that it is a resonable start to use for this problem as well.
On top of the convolutional layers I take a dense layer which just weighs 512 features that are extracted. And then there is another dense layer for the activation into the six different digits that are actually present in the captchas.
The network generation is done in a function because I have different input shapes. In the book it is described that the input size can also be variable, but this seems to be easier for a start.
def make_network(shape): network = keras.models.Sequential() network.add(keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=shape)) network.add(keras.layers.MaxPooling2D((2, 2))) network.add(keras.layers.Conv2D(64, (3, 3), activation='relu')) network.add(keras.layers.MaxPooling2D((2, 2))) network.add(keras.layers.Conv2D(128, (3, 3), activation='relu')) network.add(keras.layers.MaxPooling2D((2, 2))) network.add(keras.layers.Conv2D(128, (3, 3), activation='relu')) network.add(keras.layers.MaxPooling2D((2, 2))) network.add(keras.layers.Flatten()) network.add(keras.layers.Dense(512, activation='relu')) network.add(keras.layers.Dense(6, activation='softmax')) return network
We then use this to create a network based on the shape of the first digit slice.
network = make_network(train_images.shape[1:]) network.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
The model is summarized by Keras in the following table:
| Layer (type) | Output Shape | Param # |
|---|---|---|
| conv2d_13 (Conv2D) | (None, 78, 52, 32) | 320 |
| max_pooling2d_13 (MaxPooling) | (None, 39, 26, 32) | 0 |
| conv2d_14 (Conv2D) | (None, 37, 24, 64) | 18496 |
| max_pooling2d_14 (MaxPooling) | (None, 18, 12, 64) | 0 |
| conv2d_15 (Conv2D) | (None, 16, 10, 128) | 73856 |
| max_pooling2d_15 (MaxPooling) | (None, 8, 5, 128) | 0 |
| conv2d_16 (Conv2D) | (None, 6, 3, 128) | 147584 |
| max_pooling2d_16 (MaxPooling) | (None, 3, 1, 128) | 0 |
| flatten_4 (Flatten) | (None, 384) | 0 |
| dense_7 (Dense) | (None, 512) | 197120 |
| dense_8 (Dense) | (None, 6) | 3078 |
And the number of parameters is 440,454 in total.
Then I fit the model and using the training data and validate with the validation data to see whether I run into overfitting.
history = network.fit( train_images, train_labels, epochs=40, batch_size=128, validation_data=(validation_images, validation_labels))
We can visualize the history of the training process with the value of the loss function as well as the accuracy on both the training and validation data. The lower gray line in the accuracy plot marks $1/6$ which would be the accuracy of guessing which of the six digits is correct. The upper one is 1, which is perfect accuracy.
After 40 epochs we obtain a training accuracy of 1.0000, which certainly smells like overfitting. But the validation accuracy is also high, so apparently we are on a good track. In order to better see it, one should plot the error ratio in a log scale. The points with perfect accuracy drop out in such a plot, so focus on the validation there.
In the end we reach a validation accuracy of 0.9980, so we clearly have a network which is general enough to solve examples that it has not seen before. Also on the separate test data we have 0.9980 accuracy.
We need to get six digits right, so the probability of getting all six digits right is $0.9980^6 = 0.9881$. This assumes that the digit recognition for the other five slices is similar, which I am willing to make. The number is impressively high given that I just took a recipe from the book and applied it without tuning the network in any way.
The training takes around 9 seconds per epoch, as we reach sufficient real world accuracy after like 25 epochs, this is done in a couple of minutes on my laptop CPU. It seems that this problem is solved just right there and the captcha is already cracked. And for the 1.2 % of the cases where we do not solve the captcha right on the first go, we just request a new one. With an error rate that low we would not raise any suspicion.
Fiddling with the network
Although there is no need to, we can investigate whether we could solve the problem with less resources. To start with, I have just shrunken the dense layer (which is part of the classifier) from 512 to 128. Also I have stopped after 30 epochs. The results in the end are virtually the same. We just happen to have an fluctuation in the 30th epoch, in the 29th it seems to have very similar accuracy on the validation data. Time has only gone down to 8 seconds per epoch, so we are not really much faster by using the smaller dense layer in the end.
Next I have tried to remove one of the blocks consisting of convolution and maxpooling layers. Interestingly the number of parameters in the model goes up to 748,934. Time is still 8 seconds per epoch, so that does not change anything. The resulting accuracy also seems to be quite okay, but it might need a few more epochs in order to get it to the level of the other ones. Interestingly there seems to be a lack of these fluctuations, I take that to be a good sign. The model likely now has less free parameters such that it learns the features better and does not learn so much from the noise.
Perhaps adding some dropout will improve the system even more. Just after the dense layer with 128 elements I have added a dropout layer with a 0.5 coefficient. It seems that it does not really improve anything.
The convolutional layer uses 3×3 tiles. The maxpooling layer then takes a 2×2 tile and takes the maximum out of that. So basically we cover a 4×4 area with one convolutional block. The next convolutional layer similarly acts the same and with $n$ blocks we have a square with side length $4^n = 2^{2n}$. The letters in the images are roughly 16 pixels of size, so we should be able to get sufficient information with just two blocks. But then the model has 1,789,190 parameters. This sound like the wrong direction. So I take two blocks, but make the last maxpooling layer to have 5×5 maxing. I already know that there is only one digit in the whole picture, so perhaps we could average over larger areas. This just takes 5 seconds/epoch to fit, but the results are horrible.
Apparently I am moving into the wrong direction. Although the features that I want to detect are small, the image where they lie on is rather large. So at the moment I do the locating of the digit with the dense network. Let us therefore go back to the four convolutional blocks. We are back at the model with 290,310 parameters now.
I want to see what happens when I use less data. So instead of using 1000 images for training, let's just use 100. There are six digits, but with rotation. So perhaps 100 would mean just 16 observations of each, that might not be sufficient to gather all the rotations. The training is much faster now as there is just 10 % of the data to process. Validation is still done with 500 images to yield the same precision there. The results are very poor compared to before:
We can also see that there is overfitting. The accuracy for the training data is much better than for the validation data. Perhaps we can try to use dropout here to regularize it and prevent it from overfitting. But as one can see in the following plot, the single dropout layer does not magically cure that there just is not enough data.
Conclusions
It is refreshingly simple to play around with deep neural networks using the Keras library. For this blog entry I have just fiddled around with it for a day, before that I read in the book.
The captcha can be solved rather quickly, no wonder that this type is not used that much any more these days.
One could likely improve the accuracy of this process further, but I just do not see a point because for all practical purposes it is more than sufficient.
You can download the source code from GitHub.