Graphentheorie in On Tour
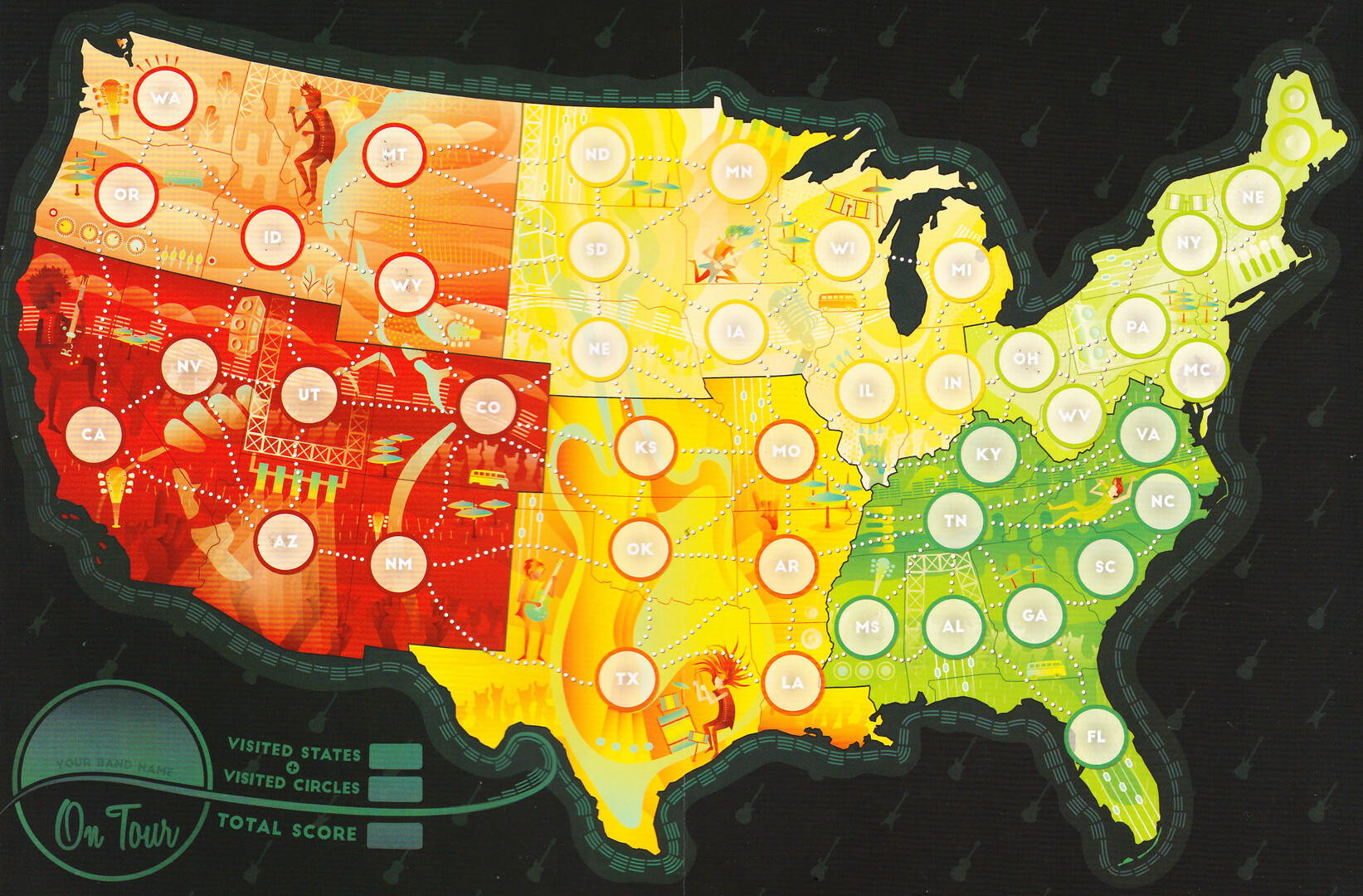
Die Tage habe ich das Spiel On Tour gespielt. Man soll eine Band-Tournee durch die USA planen. Dabei hat man als Spielbrett diese Landkarte. In die einzelnen Staaten trägt man dann gewürfelte Zahlen ein. Man würfelt mit zwei W10 und setzt die beiden Ziffern in beiden Kombinationen zusammen. Würfelt man 1 und 5, so muss man die 15 und 51 eintragen. Es ist noch ein wenig eingeschränkt, wohin man diese eintragen darf.
Sind alle Felder mit Zahlen voll, so muss man die Städte verbinden. Dabei darf man jeden Staat nur maximal einmal besuchen, und man darf nur Zahlen verbinden, die nicht absteigend sind (gleich ist okay). In meinem Kopf verschwindet die Landkarte, und es bleibt nur noch ein ungerichteter Graph übrig, der so aussieht:
Man trägt nun im nächsten Schritt die Zahlen ein. Man versucht die Zahlen schon so einzutragen, dass man am Ende eine möglichst lange Tour verbinden kann. Man bekommt pro Stopp in der Tour einen Punkt. Dadurch, dass man nur zu höheren oder gleichen Zahlen weiterfahren kann, wird der Graph effektiv gerichtet. Ich habe hier einfach zufällig die Zahlen von 0 bis 40 eingetragen. Die Verbindungen sind jetzt gerichtet, immer von der kleinen zur großen Zahl:
Nun möchte man den längsten einfachen Pfad in diesem Graphen finden. Das ist für allgemeine Graphen ein NP-Problem, also eines, das extrem viel Rechenzeit braucht, sobald das Problem groß wird. Sind die Zahlen allerdings erstmal reingeschrieben, so kann man in linearer Zeit den längsten Weg finden.
Die Schwierigkeit im Spiel ist allerdings nicht am Ende den längsten Pfad zu finden, sondern die zufällig gewürfelten Zahlen in die zusätzlich zufällig bestimmten Regionen (Norden, Süden; Westen, Mitte, Osten) einzutragen. Man kann also nicht unbedingt damit planen, dass alle Zahlen kommen, oder die richtigen Zahlen an die richtige Stelle schreibbar sind. Dadurch bekommt das Spiel wieder viel Zufall, mit dem man nicht so wirklich planen kann.