Clusting Recorded Routes
I record a bunch of my activities with Strava. And there are novel routes that I try out and only have done once. The other part are routes that I do more than once. The thing that I am missing on Strava is a comparison of similar routes. It has segments, but I would have to make my whole commute one segment in order to see how I fare on it.
So what I would like to try here is to use a clustering algorithm to automatically identify clusters of similar rides. And also I would like find rides that have the same start and end point, but different routes in between. In my machine learning book I read that there are clustering algorithms, so this is the project that I would like to apply them to.
Incidentally Strava features a lot of apps, so I had a look but could not find what I was looking for. Instead I want to program this myself in Python. One can export the data from Strava and obtains a ZIP file with all the GPX files corresponding to my activities.
Reading the data
The activities are just numbered, so one needs to look up the meta data in activities.csv, which looks like this:
I might resolve that at some point, but at first the labeling of the data is irrelevant.
The coordinates given in the GPX data is latitude and longitude. I always get them confused as I rather think in North-South and West-East or spherical coordinates $\theta$ and $\phi$. So the coordinates that we have here are these:
| Term | Symbol | Direction |
|---|---|---|
| Latitude | $\phi$ | North-South |
| Longitude | $\lambda$ | West-East |
When one knows the earth radius one can provide an approximate mapping to $x$, $y$ and possibly $z$ coordinates. I can easily provide this assuming a fixed radius of the earth. But as I am only moving around in a rather localized environment, I could just approximate with a tangent plane and take latitude and longitude as coordinates. This will effectively be a Mercator projection, which we are used to anyway. Distances are not exactly what they seem and need to be corrected with a cosine factor depending on the latitude. For comparing points with each other, this is sufficient.
As all the machine learning libraries are implemented in Python, I need to load the data into Python. There is the gpxpy library which can read it in the GPX files from Strava. It provides a nice list, and that is all I need.
Clustering by start or end points
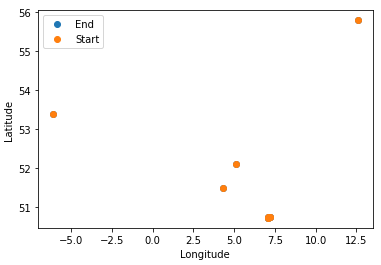
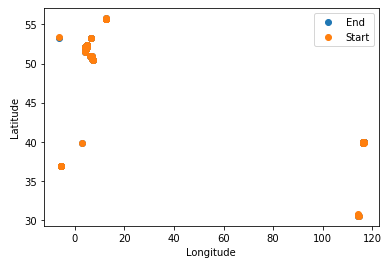
At first I have only loaded 10 data points. And plot latitude and longitude, not worrying about the non-distance preserving projection.
I then zoom in onto the region where I deem the largest cluster, that likely is the Bonn cluster.
In my machine learning book it has a section of clustering algorithms. I will first try the K-Means and then the DBSCAN to see how they perform on this problem.
K-Means
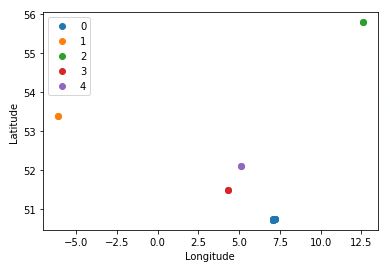
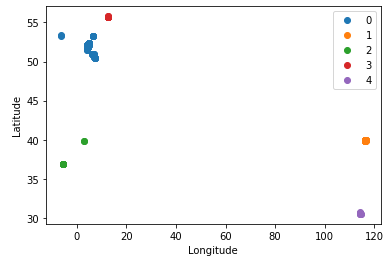
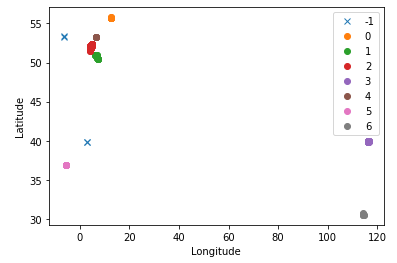
The first clustering algorithm that I read about is the K-Means one. It is implemented in SciKit-Learn, but has the drawback that one needs to know the number of clusters beforehand. I take the above subset of data and let it cluster into 5 clusters, as these are the ones that I can see by eye. I color them and it works just as one would expect.
In the meantime I have loaded the full data set, this looks like that:
One can see the big cluster around Bonn, then there is a cluster in the Netherlands, around København (DK), Spain and Italy. Also the two clusters in China can be seen. What happens now when I let it find five clusters? The clusters are (0) Germany and Netherlands, (1) Beijing, (2) Spain and Italy, (3) København and (4) Wuhan.
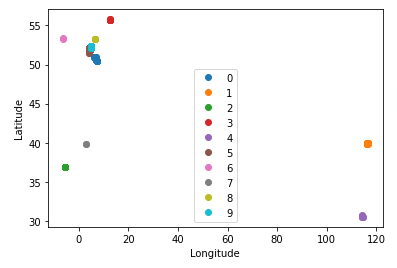
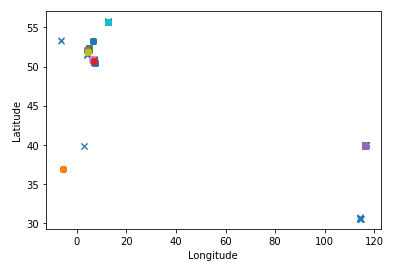
That's nice, but I would like to find clusters on a fixed say 200 m scale, and not just the top $n$ clusters. But let us try to explore this a bit more. Letting it find 10 clusters, one can see that Spain (green) and Italy (gray) have been split up. Also the Netherlands (pink) were split off. And the main cluster shows that there is a chunk around Bonn and then also more in other cities north of that.
Zooming into the Bonn region again, we can see how that is still just one cluster. And although I am not perfectly sure, I think that I can make out a few points of interest just from the clusters.
DBSCAN
The DBSCAN algorithm defines clusters in a much more fitting way. Instead of trying to find $k$ clusters, it uses a measure of distance $\epsilon$ and a minimum number of samples $n$ to define core instances. A core instance is a data point which has $n$ other instances within a distance of $\epsilon$. Core instances may be connected into the same cluster.
I have first tried $\epsilon = 1.0$ and $n = 3$, as I am not sure how that works. I presume that it uses $\epsilon \leq \sqrt{\phi^2 + \lambda^2}$, but I am not sure. In that case a whole degree is super coarse grained. But it works much better than before. See how there are three distinct regions in the main clustering region now. The algorithm also puts anomalies when there are no neighbors. I now actually think that I misinterpreted the points before. The single anomaly in the north is Ireland, the red stuff is the Utrecht and Holland, the brown one is Groningen. The one in Italy is an anomaly (because I just recorded one there), whereas in Spain I have multiple ones.
This is very promising! I will need to decrease the $\epsilon$ value somehow. Looking at the map around my flat I feel that $\epsilon = 0.00350$ would make for a couple hundred meters. And indeed, using this as a measure of distance I get so many clusters that the legend becomes pointless.
Zooming into the Bonn region, I can see that there are more sensible clusters now. The big green one likely is my place of living, and then there are other ones that I cannot exactly make out. It will be interesting to see this combined with a map at some point.
There are now 23 clusters. One of them makes up 149 observations, and there are 88 anomalies. That sounds like a pretty good start! Perhaps I need to decrease the distance measure a little bit or increase the number of observations before it counts as a cluster. Using the same $\epsilon$ but $n = 5$ for instances reduces the number of clusters to 13, the largest cluster still has 149 observations but there are now 124 anomalies. Perhaps this is even better.
So far I have just thrown start and end point together. This would allow to identify points where I have either started or finished, but it does not really allow to classify actual routes. So I have changed the data from two numbers (latitude and longitude) to four (lat/lon for start/finish). This way it becomes a four dimensional clustering problem and I cannot visualize it neatly any more.
I can show the starting points of the new clusters. Then one can see that there are ones where apparently I have started at home and ended at home, and ones where I have started at home but ended at the other cluster of points. All other points became anomalies now. There are only 7 clusters in the whole data set now.
Metric for tracks
Clustering by the start and end points is neat, I so have for instance all commutes to work in one cluster. But what happens with the ones where I made a detour? Sometimes I try slightly different paths on a commute and I would like to cluster them on a finer level. For this we need to take a look at the whole route, not just at the start and end point.
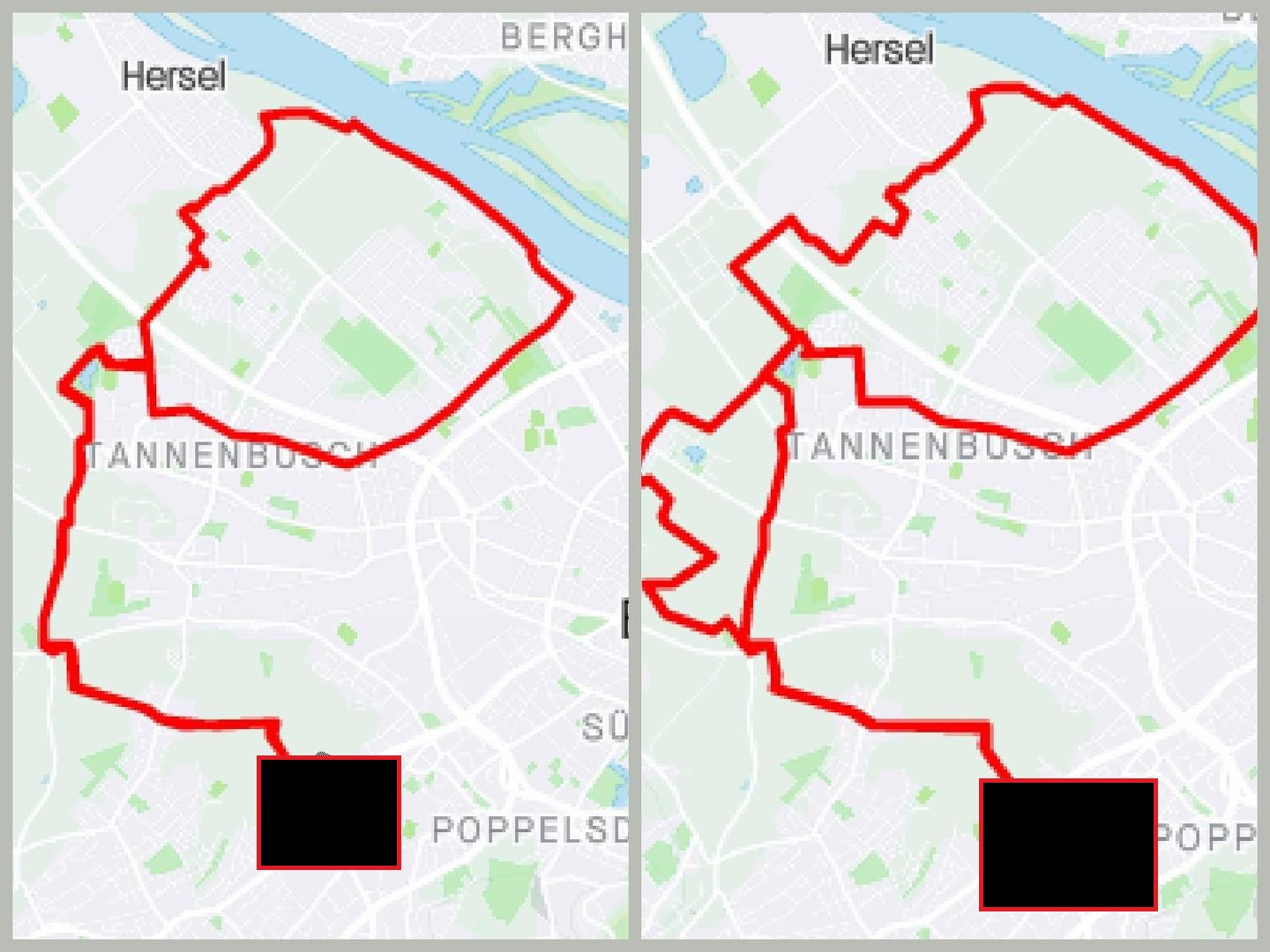
The algorithms need to know the distance between elements. So I need to define a metric in the space of whole tracks. The intuitive way is to just plot a pair of tracks on a map and look at it. The following picture shows two different tracks that were recorded on the same route. There are slight deviations from GPS inaccuracies. But we would still say that this was the same route.
Map from Open Street Map. Track visualized in Viking.
In my program we don't have the pattern recognition machine that is our brain. So there is a need for something that can actually be computed. Zooming in shows the actual points in the track. As a metric, it seems sensible to compute the distance from each point to the other track. Just trying to use the points in order does not work because sometimes I walk slower or faster, and then the distances would be much larger. Also the number of points in the recording does not always match, and sometimes different programs use different recording intervals. One really needs to match the points with each other.
Map from Open Street Map. Track visualized in Viking.
For this we need to compute the distance from every point of the green track to the orange track in the form of a distance matrix $$ D_{ij} = \sqrt{ \cos\left( \frac{\phi_i^{(1)} - \phi_j^{(2)}}{2} \right)^2 (\lambda_i^{(1)} - \lambda_j^{(2)})^2 + (\phi_i^{(1)} - \phi_j^{(2)})^2 } \,. $$ The cosine term is needed because differences in longitude $\lambda$ mean different linear distance depending on the latitude $\phi$. This likely won't pose a big problem, but it is cleaner to include here.
I take the minimum value from each row, and also from each column. These are the minimum distances of each track to the other one. Then I take the sum of both means to yield the distance. This can be multiplied with the earth radius to give the average distance between corresponding points in the track. As a mathematical expression, this would be $$ g_{1,2} = r_{\mathrm{Earth}} \cdot (\mathrm{mean}i \min_j D + \mathrm{mean}j \min_i D) \,. $$
For the given two walks I obtain a distance measure of around 0.6 m, which makes sense. For two random ones I obtain like 1000 km, which isn't surprising with one being in Denmark and the other one in Bonn.
The documentation of DBSCAN states that one can supply a precomputed distance matrix. This way we can just pass our custom metric $g_{ab}$ that we have defined above.
The metric is implemented using NumPy arrays and seems to take 31 ms per call, so with currently 224 activities it would take like 20 min to compute it all. That seems wasteful as we already have the clusters from the start and end points. We can then use all the tracks within one cluster of start and end points to compute the distance, doing a sub-cluster detection using that data. The problem is that within each cluster there are still a lot of activities. In the cluster around my home there are more than half of the activities, which is not really a surprise.
I have tried to thin out the points before feeding them into the metric. This does not work, because then the average distance between the points increases and the metric value becomes less meaningful. So perhaps there is no way to save processing power there. Computing the distance between all tracks in a cluster is an $\mathrm O(n^2)$ operation and quite lengthy.
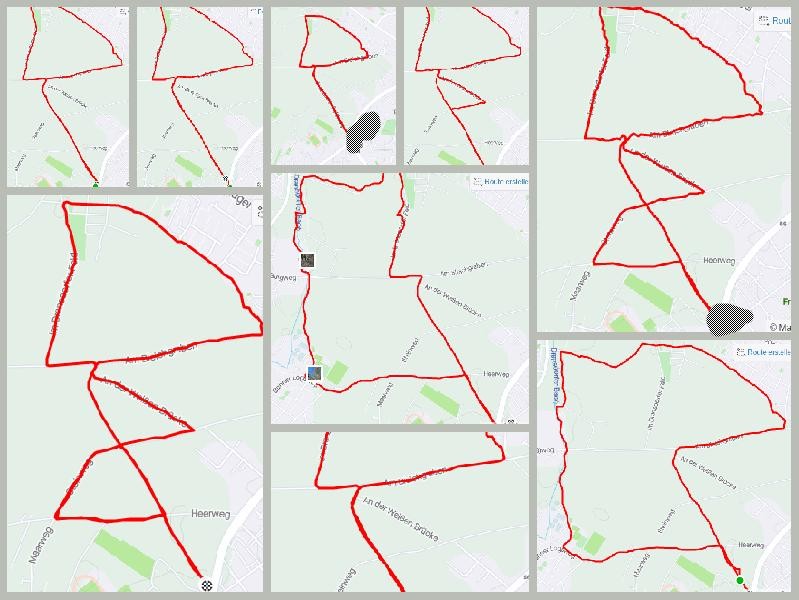
Sub-clustered tracks
Using the above procedure I have created sub-clusters from each start-end cluster using an $\epsilon = 5.0\,\mathrm{m}$. The clusters look somewhat sensible.
For instance a round course that I do through the woods. I have done it slightly differently twice, and the algorithm has identified those.
Or I have another round that I do to the Rhine river. There it spotted two instances of that.
Then I have another through the fields, which apparently I have recorded three times.
And the walk through the field right next to my door.
I would find that it works reasonable well, depending on the intention.
Refining the metric
One could however argue that the metric is not fine-grained enough. One can see that often routes are put into the same cluster if they have some of the path in common. These segments bring down the average distance and allow for larger deviations in other parts. This will make some sort of similarity in routes. There is always something in common such that the distance is measured below the threshold.
But this is not what I had mind. I actually would like to have each distinct shape in its own category. So instead of taking the mean distance between points, I would rather go for the maximum. This would the largest deviation in the route. The problem is that sometimes the GPS produces one or two outlier points. Therefore it would be better to not take the maximum, but like the third largest distance and use that as a metric. This would be outlier safe. Otherwise one could use some particular quantile. Taking the sum of distances will not work due to the noise or systematic shifts. These would just build up as the routes get longer, giving a rather bad number. Using np.partition I can get the second largest element from each and use the sum as a metric.
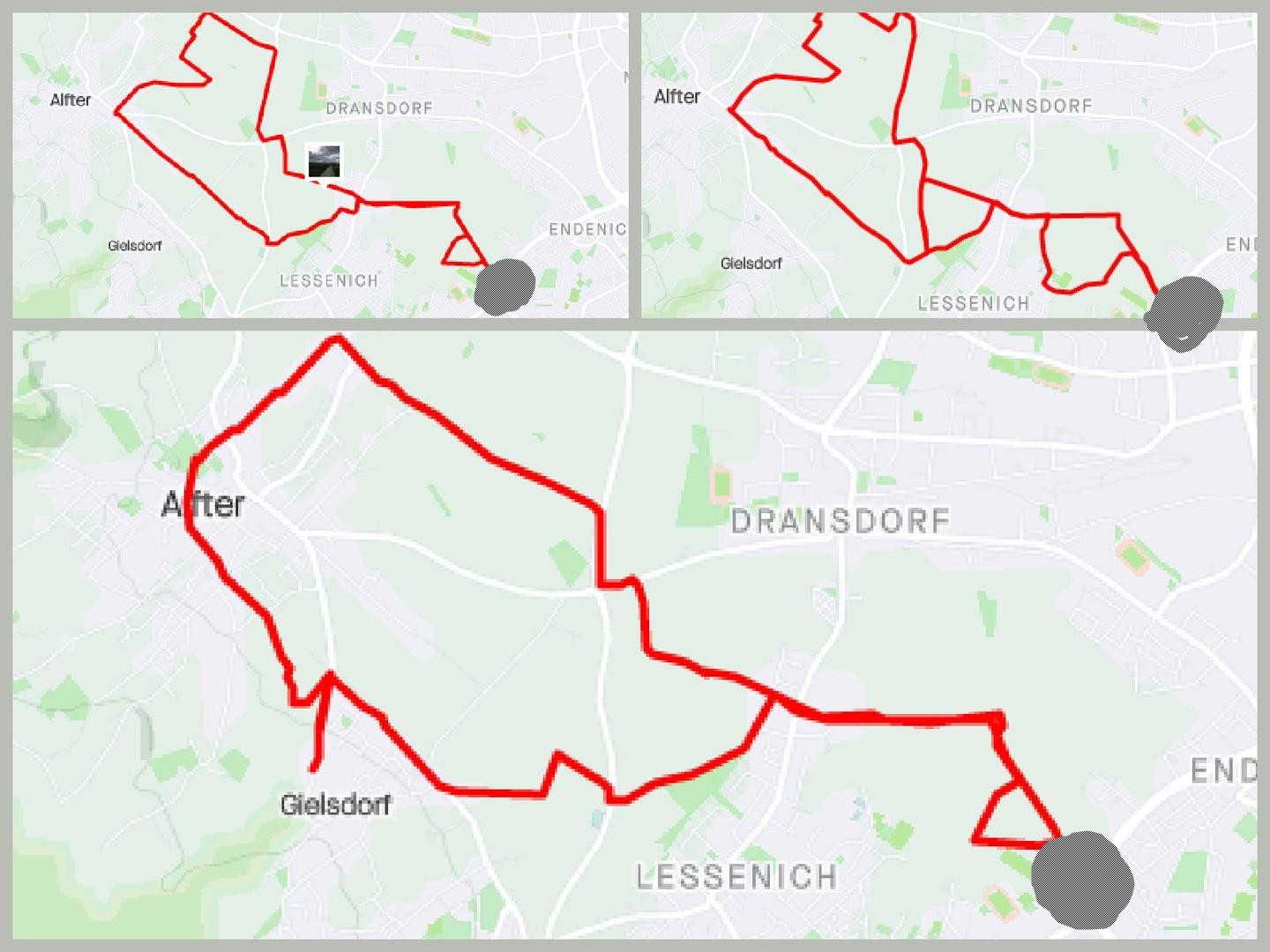
Using this new definition it can distinguish between routes where I have taken a detour and the ones where I have not.
So from the walks to the air field in Hangelar now only these are within the same cluster. And the one with the little detour is gone, just like I wanted it.
Conclusion
It seems possible to automatically find clusters of whole tracks in this way. The performance with the metric that I have defined is not so awesome, and also the $\mathrm O(n^2)$ runtime is not perfect. Having something of order $\mathrm O(n \log n)$ would be much preferred, but then I would have to find something that would allow me to prevent comparing every track in a cluster with every other one.
Using the now determined clusters and sub-clusters I could do more analysis or create just a list of links. The clusters could be given names such that it would be more meaningful.
Strava actually offers this as a paid feature I just realized. Apparently there is some interest in it!
I might embellish this in the future. This has been a nice project to try out clustering algorithms.